Fonctions convexes d`une variable réelle

Fonctions convexes d'une variable réelle
© S. DUCHET - www.epsilon2000.fr.st
1/11
F
FO ON NC CT TI IO ON NS S C CO ON NV VE EX XE ES S D D' 'U UN NE E V VA AR RI IA AB BL LE E R RE EE EL LL LE E
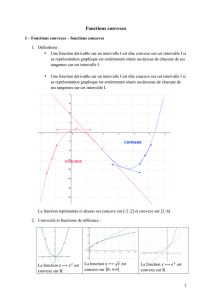
1 Notion de fonction convexe
1.1 Théorème fondamental
Soit f une fonction numérique définie sur un intervalle I de \. Les assertions suivantes sont
équivalentes :
(i) , , [0;1],( (1)) ()(1)()
x
yI t ftx ty tfx tfy∀∈∀∈ +− ≤ +− .
(ii) () () () () () () ,, ,( )
f
yfxfzfxfzfy
xyz I x y z yx zx zy
−−−
∀∈<<⇒ ≤ ≤
−−−
.
(iii) () ( )
,
f
tfa
aIt ta
−
∀∈ − 6 est croissante sur
{
}
\
I
a.
(iv)
111
,, ,( ) 0
() () ()
xyz I x y z x y z
fx fy fz
∀∈<<⇒ ≥
.
(v) L'ensemble
{}
2
(;) / ()
A
xy x Ietfx y=∈∈ ≤\ (appelé épigraphe de f )
est une partie convexe de 2
\.
Démonstration
() ( )iii⇒
Soient ,,
x
yz I∈ tels que
x
yz<<
. Il existe 0]0;1[t
∈
tel que 00 (1 )ytx tz
=
+− .
Alors 0yz
t
x
z
−
=− et 0
1
x
zyzxy
t
x
zxz xz
−−−
−= − =
−− −
.
D'après (i) :
00
() () (1 )()
f
ytfx tfz≤+−
() () ()
yz xy
f
yfxfz
xz xz
−−
≤+
−−
(1.1)
() () 1 () ()
yz xy
f
yfx fx fz
xz xz
−−
⎛⎞
−≤ − +
⎜⎟
−−
⎝⎠
() () () ()
yx xy
f
yfx fx fz
xz xz
−−
−≤ +
−−
() () () ()
yx yx
f
yfx fx fz
zx zx
−−
−≤− +
−−
Donc () () () ()
f
yfx fzfx
yx zx
−−
≤
−−
.
En reprenant la relation (1.1), on a :
() () () 1 ()
⎛⎞
−−
⎟
⎜
−≤ +−⎟
⎜⎟
⎟
⎜
⎝⎠
−−
yz xy
f
yfz fx fz
xz xz

Fonctions convexes d'une variable réelle
© S. DUCHET - www.epsilon2000.fr.st
2/11
() () () ()
yz yz
f
yfz fx fz
xz xz
−−
−≤ −
−−
() () () ()
f
yfz fxfz
yz xz
−−
≥
−−
(division par 0yz−<)
donc () () () ()
f
zfx fzfy
zx zy
−−
≤
−−
() ( )ii iii⇒
Soient
{}
12
,\tt I a∈, avec 12
tt<.
Si 12
0tt<<, on applique le (ii) avec 12 (,,) (, ,)
x
yz t t a=.
Si 12
tat<<, on applique le (ii) avec 12 (,,) (,, )
x
yz t at=.
Si 12
at t<<, on applique le (ii) avec 12 (,,) (,, )
x
yz at t=.
() ()iii iv⇒
Soient ,,
x
yz I∈ tels que
x
yz<<.
111 1 0 0
() () () () () () () ()
xyz x yx zx
f
xfyfz fxfyfxfzfx
=−−
−−
()()
( ) () () ( ) () ()y x fz fx z x fy fx=−−−−−
() () () ()
()() ()()
f
zfx fyfx
yxzx zxyx
zx yx
−−
=−− −−−
−−
() () () ()
()()
f
zfxfyfx
yxzx zx yx
⎡⎤
−−
⎢⎥
=−− −
⎢⎥
−−
⎣⎦
Le crochet est positif d'après (iii). Le déterminant est un produit de quantités positives donc est
positif.
() ()iv i
⇒
Soient ,
x
yI∈. Supposons
x
y≤. Soit [0;1]t∈.
D'après (iv),
111
(1 ) 0
() ( (1 )) ()
xtx tyy
fx ftx ty fy
+−≥
+−
Nous allons effectuer les opérations sur les colonnes : 221 3
(1 )cctc tc←− −− , ce qui ne changera
pas la valeur du déterminant :
101
00
() ( (1)) ()(1)() ()
xy
fx ftx ty tfx tfy fy
≥
+−− −−
()
( )( (1)) ()(1)() 0yxftx ty tfx tfy−− +−− −− ≥
donc ( (1 ) ) ( ) (1 ) ( ) 0ftx ty tfx tfy
+−− −− ≤
donc ( (1 ) ) ( ) (1 ) ( )
f
tx t y t f x t f y+− ≤ +−
donc f vérifie (i).
Si yx
≤, on change t en (1 )t− pour obtenir le résultat.

Fonctions convexes d'une variable réelle
© S. DUCHET - www.epsilon2000.fr.st
3/11
() ()iv⇒
Soient 11
(;)
x
y et 22 (;)
x
y deux éléments de 2 \ tels que 12 ,
x
xI∈ et 11 ()
f
xy≤ et 22 ()
f
xy≤.
Notons A l'ensemble
{}
2
(;) / ()Axy xIetfxy=∈∈ ≤\.
Soit [0;1]t∈. Montrons que
()
1212
(1 ) ; (1 )tx t x ty t y A+−+−∈.
12
(1 )tx t x I+−∈ car 1
x
I∈, 2
x
I∈ et I est un intervalle de \.
()
121 2
(1 ) ( ) (1 ) ( )
f
tx t x tf x t f x+−≤ +−
12
(1 )ty t y≤+−
donc
()
1212
(1 ) ; (1 )tx t x ty t y A+−+−∈.
() ()vi⇒
Soient ,
x
yI∈et [0;1]t∈.
()
;()
x
fx A∈ et
()
;()yfy A∈. A étant une partie convexe de 2 \, on a :
()
(1 ) ; ( ) (1 )tx t y tf x t y A+−+−∈ donc
()
(1 ) ( ) (1 ) ( )
f
tx t y tf x t f y+−≤ +−.
1.2 Fonction convexe
Soit f une fonction numérique définie sur un intervalle I de \. Si f vérifie l'une des assertions du
théorème précédent, on dit que f est convexe sur I. On dit que f est concave si
()
f
− est convexe.
Conséquences
Une combinaison linéaire de fonctions convexes est convexe (conséquence immédiate de (i)).
Si f est convexe sur un intervalle I de \, et si g est une fonction croissante sur I, alors gfD est
convexe (conséquence de (ii)).
1.3 Proposition
Soit f une fonction définie sur un intervalle I de \.Alors f est convexe si et seulement si pour tout
système de points 1
()
iin
x≤≤ de I et tout système 1 ()
iin
a
≤
≤ de réels positifs vérifiant 11
n
k
ka
=
=
∑, on a :
11
()
nn
kk k k
kk
f
ax a f x
==
⎛⎞
≤
⎜⎟
⎝⎠
∑∑ .
Démonstration
La condition est suffisante car pour 2n
=
, on retrouve le (i) du théorème fondamental. Montrons
que la condition est nécessaire.
Notons ( )Pn la propriété "pour tout système de points 1
()
iin
x
≤
≤ de I et tout système 1
()
iin
a≤≤ de réels
positifs vérifiant 11
n
k
ka
=
=
∑, on a : 11
()
nn
kk k k
kk
f
ax a f x
==
⎛⎞
≤
⎜⎟
⎝⎠
∑∑ ".
(1)P est vraie
(2)P est vraie (condition (i) du théorème fondamental)

Fonctions convexes d'une variable réelle
© S. DUCHET - www.epsilon2000.fr.st
4/11
Supposons ( )Pn vraie pour 2n≥.
Soient 11
()
kkn
x≤≤+ un système de points de I et 11 ()
kkn
a
≤
≤+ un système de réels positifs vérifiant
1
11
n
k
ka
+
=
=
∑.
Si 10
n
k
ka
=
=
∑, alors 0
k
a= pour tout k tel que 1kn
≤
≤ et l'inégalité est vérifiée car (1)P est vraie.
Si 10
n
k
ka
=
≠
∑, posons 1
n
k
ka
λ
=
=
∑
et 1
1n
kk
k
yax
λ
=
=∑.
()
1
11
1
n
kk n n
k
f
ax f y a x λ
+
++
=
⎛⎞
=+
⎜⎟
⎝⎠
∑
11
() ( )
nn
f
yafx
λ
++
≤+ (car (2)P est vraie)
11
1() ( )
nkkn n
k
a
f
xafx λλ
++
=
≤+
∑ (car ( )Pn est vraie)
1
1()
n
kk
kafx
+
=
≤∑
Donc (1)Pn+est vraie.
Donc ()Pn est vraie pour tout entier *
n∈`.
2 Continuité et dérivabilité des fonctions convexes
2.1 Théorème
Soit f une fonction convexe sur un intervalle I de \. Alors f admet une dérivée à droite et une
dérivée à gauche en tout point a intérieur à I et ''
() ()
gd
f
afa≤. f est continue sur
I
D. D'autre part, si
,ab I∈
D et ab<, alors ''
() ()
() ()
dg
fb fa
f
afb
ba
−
≤≤
−. Enfin, '
g
f
et '
d
f
sont des fonctions croissantes
sur
I
D.
Démonstration
Soit aI∈
D. Soit 0
tI∈ tel que 0 ta>. D'après le (iii) du théorème 1.1, on a :
0
0
() ()
() ( )
f
tfa
ft fa
ta t a
−
−≤
−−
pour 0 tt≤. d'après le théorème de la limite monotone, l'application
() ( )
:
a
f
tfa
tta
φ
−
−
6 admet une limite à gauche en a donc f est dérivable à gauche en a et
'0
0
() ()
()
g
f
tfa
fa ta
−
≤−. Cette dernière inégalité étant vraie pour tout 0
ta>, 0 tI∈, on en déduit, par
application du théorème de la limite monotone que a
φ
admet une limite à droite en a et donc
''
() ()
gd
f
afa≤.

Fonctions convexes d'une variable réelle
© S. DUCHET - www.epsilon2000.fr.st
5/11
f étant dérivable à gauche et à droite en a, on en déduit que f est continue à gauche et à droite en a.
Donc f est continue en a.
Soient ,
ab I∈
D, avec ab<. d'après ce qui précède :
'() ( )
() inf
dtI
ta
f
tfa
fa ta
∈
>
−
=− donc '() () ()
d
f
bfa
fa ba
−
≤−
'() () ( ) ()
() sup sup
gtI tI
tb tb
f
tfb fbft
fb tb bt
∈∈
<<
−−
==
−−
donc '
() () ()
g
fb fa
f
b
ba
−
≤
−
Donc '' ''
() ()
() () () ()
gd gd
fb fa
f
afa fbfb
ba
−
≤≤ ≤≤
−.
Remarque : Il existe des fonctions convexes et non continues, par exemple :
:[0;1]
00 1
01
11
f
x
si x
→
<<
\
6
6
6
2.2 Théorème
Soit f une fonction dérivable sur un intervalle I de \. Alors f est convexe sur I si et seulement si f '
est croissante sur I.
Démonstration
Supposons f convexe sur I. Soient ,ab I
∈
avec ab
<
. le théorème 2.1 indique que '' () ()
dg
f
afb≤.
Or f est dérivable en a et b donc '() '()
d
f
afa= et '() '()
g
f
bfb=. f ' est donc croissante sur I.
Supposons maintenant f ' croissante sur I.
Soient 12
,
x
xI∈, avec 12
x
x< et ]0;1[t∈ (le cas 0t
=
et 1t
=
est toujours vrai dans le (i) du
théorème fondamental).
Posons 12
(1 )
x
tx t x=+− (on a 12
x
xx<< ).
D'après le théorème des accroissements finis :
Il existe 11
];[cxx∈ tel que 111 () ( ) ( ) '( )
f
xfx xxfc−=−
Il existe 22
]; [cxx∈ tel que 222 () ()( )'()
f
xfxxxfc−=− .
Alors 1
11
() ( )
'( )
f
xfx
fc xx
−
=− et 2
22
() ()
'( )
f
xfx
fc xx
−
=−.
f ' étant croissante sur I, on a 12 '( ) '( )
f
cfc≤, c'est-à-dire 12
12
() ( ) ( ) ()
f
xfx fx fx
xx x x
−
−
≤
−−
.
121
(1 )( )
x
xtxx−=− −
221
()
x
xtx x−= −
Alors 121
21 21
() () () ()
(1 )( ) ( )
f
xfx fx fx
tx x tx x
−−
≤
−− −