Connaitre le cosinus, le sinus, la tangente d`un angle aigu

Mathématiques en classe de 3ème au collège Haxo – S.Percot
CHAPITRE)7):)Trigonométrie!
!
Les)compétences)travaillées):))
!"##$%&'()*()+",%#-,.)*(),%#-,.)*$)&$#/(#&()01-#)$#/*()$%/-)2"34)5678)9:7;<)
!$*+-*(')-#()*"#/-(-')9$')&'%/"#"=>&'%()2"34)56?8)9:76<))
@>&('=%#(')-#)$#/*()9$')&'%/"=>&'%()2"34)56A8)9:77<))
)
I):)Connaitre)le)cosinus,)le)sinus,)la)tangente)d'un)angle)aigu))
)
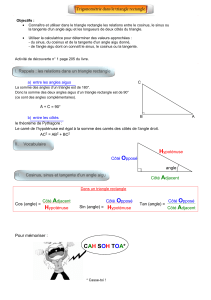
Définition):)Dans!un!triangle!rectangle,!pour!un!angle!aigu!donné,!on!définit!trois!rapports!de!longueurs!:!
!
Le!sinus!de!cet!angle!qui!est!égal!au!quotient!:
Côté à cet angle aiguopposé
Hypoténuse
!
!
Le!cosinus!!de!cet!angle!qui!est!égal!au!quotient!:!
Côté à cet angle aiadjacent
Hypot
gu
énuse
!
!
La!tangente!de!cet!angle!qui!est!égale!au!quotient!:!
Côté à cet angle aigu
Cô
opposé
adjacenté à cet antgle aigu
!
)
)
Exemple):)Dans!un!triangle!ABC!rectangle!en!A,!!on!a!donc!:!
sin ACB
!
=AB
BC
! !
cos ACB
!
=AC
BC
! !
tan ACB
!
=AB
AC
)
!
Remarque):)Les!calculatrices!donnent!de!très!bonnes!valeurs!
approchées!de!ces!rapports.!Il!faut!simplement!vérifier!qu’elles!sont!
bien!configurées!en!«!Degrés!».!Par!exemple,!pour!le!cosinus!de!68°!:!
!
!
Propriété):)Dans!un!triangle!rectangle,!le!cosinus!et!le!sinus!d’un!des!angles!aigus!est!toujours!compris!entre!0!
et!1.!
)
Remarque):)En!effet,!dans!un!triangle!rectangle,!l’hypoténuse!est!le!plus!grand!côté!donc!le!rapport!entre!l’un!
des!deux!autres!côtés!et!l’hypoténuse!est!toujours!compris!entre!0!et!1.!
!
Propriété):)Dans!un!triangle!rectangle,!pour!tout!angle!aigu!de!mesure!B!:!
( ) ( )
22
sin cos 1xx+=
!!!!!
sin
tan
cos
x
x
x
=
!
!
5B('+%+(,)0-)=$#-(*)*%>,)C)+(&&()#"&%"#)8))
))))))5B('+%+(,)D)C)D?)9$/():7;)E):7D)
!
!
!)

II):)Calculer)la)longueur)d’un)côté)d’un)triangle)rectangle)
Pour!calculer!un!côté!d’un!triangle!rectangle!dont!on!connait!un!angle!aigu!et!la!longueur!d’un!côté!il!faut!:!
!
5B('+%+(,)0-)=$#-(*)*%>,)C)+(&&()#"&%"#)8)) )
)))))))))))))))))))5B('+%+(,)D)C)D?)9$/():77)E):7?)
5B('+%+(,)0-)=$#-(*)*%>,)C)+(&&()#"&%"#)8))
))))))5B('+%+(,)D)C)D7)9$/():76E:7:)
)
III):)Déterminer)la)mesure)d’un)angle)dans)un)triangle)rectangle)
Pour! déterminer! la! mesure! d’un! angle! aigu! d’un! triangle! rectangle! dont! on! connait! les! longueurs! de! deux!
côtés!il!faut!:!
)
E)F$%'()-#),+G>=$)0-)&'%$#/*()(#)
9'>+%,$#&)H-(*,)+I&>,),"#&)
*JGK9"&>#-,(.)*()+I&>)"99",>)C)*J$#/*()
+"##-)(&)*()+I&>)$04$+(#&)C)*J$#/*()
+"##-L)
)
E)5#,-%&()%*)M$-&),()0(=$#0(')H-(*)(,&)
*()+I&>)+G('+G>)(&)H-(*)(,&)*()+I&>)
+"##-L)
)
E)N*)M$-&)>+'%'()-#()>/$*%&>)$O(+)*()
'$99"'&)H-%)M$%&)%#&('O(#%')+(,)0(-B)
+I&>,L)
)
E)P#)$)$%#,%)-#()>H-$&%"#)C)-#(),(-*()
%#+"##-()2*()+I&>)+G('+G><)H-J%*),-MM%&)
0()'>,"-0'(L!
Par!exemple!:!
pour!calculer!!
AC!dans!le!triangle!!
ABC!rectangle!en!A.!
!
!
!
!
!
C’est!le!sinus!qui!fait!intervenir!à!la!fois!l’hypoténuse!et!le!côté)
opposé!à!l’angle.!On!peut!donc!écrire!:!
sin B
!
=AC
BC
!d’où! !
AC
sin 29°
6
=
!
et!donc!
6 sin 29°AC =×
!
La!calculatrice!connait!une!valeur!approchée!de!
sin 29°
!
!
!
donc!
2, 9AC ≈
cm!
!
E)F$%'()-#),+G>=$)0-)&'%$#/*()(#)
9'>+%,$#&)H-(*,)+I&>,),"#&)*JGK9"&>#-,(.)
*()+I&>)"99",>)C)*J$#/*()+"##-)(&)*()
+I&>)$04$+(#&)C)*J$#/*()+"##-L)
)
)
E)5#,-%&()%*)M$-&),()0(=$#0(')H-(*,),"#&)
*(,)0(-B)+I&>)+"##-,L)
)
)
E)N*)M$-&)>+'%'()-#()>/$*%&>)$O(+)*()
'$99"'&)H-%)M$%&)%#&('O(#%')+(,)0(-B)
+I&>,L)
)
)
E)P#)$)$%#,%)-#()>H-$&%"#)C)-#(),(-*()
%#+"##-()2*J$#/*()+G('+G><)0"#&)"#)
9"-''$)&'"-O(')-#()O$*(-')$99'"+G>()
/'Q+()C)*$)+$*+-*$&'%+(L!
Par!exemple!!
pour!déterminer!la!!
mesure!de!l’angle!
B
!
!!
dans!le!triangle!ABC!!
rectangle!en!A.!
!
!
!
!
!
!
!
C’est!le!cosinus!qui!fait!intervenir!à!la!fois!l’hypoténuse!et!le!
côté)adjacent!à!l’angle.!On!peut!donc!écrire!:!
!
cos B
!
=AB
BC
!d’où! !
cos B
!
=11
15
!
La!calculatrice!sait!alors!retrouver!une!valeur!approchée!de!
B
!
!:!
!
!
donc!
B
!
≈43°
!
!