Projet de Simulation Point de Lagrange L1 et L2

Projet de Simulation
Point de Lagrange L1 et L2
GIELARA Krystian
2014-2015 1/9

Sommaire
Introduction 3
1) Calcul de la position du point de Lagrange L1 3
2) Calcul de la position du point de Lagrange L2 4
3) Simulation de trajectoire 4
a - Trajectoire de la Terre 5
b - Trajectoire d'un satellite au point L1 et L2 6
c - Instabilité de la méthode d'Euler 8
Conclusion 9
Sources 9
2014-2015 2/9

Introduction
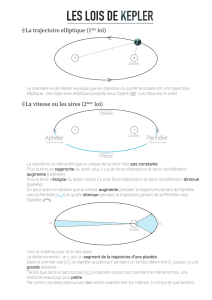
Les points de Lagrange sont des points de l'espace où les forces de gravitation
générées par 2 corps de masse non négligeable se compensent. Nous considérerons ici le
système Terre-Soleil qui comporte 5 points de Lagrange (L1, L2, L3, L4, et L5)
Nous nous intéresserons dans notre cas uniquement aux points de Lagrange L1 et L2,
qui se situent sur l'axe Terre-Soleil. En plaçant un objet en un de ces points avec une vitesse
nulle, celui-ci resterait en place indéfiniment, tout en accompagnant la rotation de la Terre
autour du Soleil avec la même vitesse angulaire.
L'intérêt d'un tel point est d'étudier par exemple les cycles solaires, en effet un
satellite placé en ce point resterait toujours entre la Terre et le Soleil, tout en restant proche
de la Terre. C'est le but de la mission SOHO.
Mon projet a donc pour objectif de chercher la position des points de Lagrange L1 et
L2, et de simuler sur un an la trajectoire d'un point en L1 et en L2.
1) Calcul de la position du point de Lagrange L1
Étant donné que tout l'aspect physique et mathématique est présent dans la
description du sujet, je m'abstiendrais de le réécrire, et ne m'occuperai que de la résolution
de l'équation finale donné ci-dessous.
A l'équilibre le point L1 obéit à l'équation :
− 1/ (1 − x)² + u / x² + 1 − (1 + u)*x = 0
avec x = distance Soleil-Point L1 / distance Terre-Soleil
Pour résoudre cette équation j'ai donc utilisé la méthode de la dichotomie qui est la
plus approprié dans ce cas de figure.
La méthode consiste à prendre un intervalle de départ, ici 0 < x < 1, car le point est
compris entre la Terre et le Soleil, de le découper en 2 et de voir dans lequel se trouve le
zéro, et ainsi de suite jusqu'à atteindre la précision voulu.
En reprenant le programme de simulation intitulé dichotomy.py, et en changeant
l'intervalle pour celui au dessus, j'obtiens x = 0,99 ce qui nous donne la distance Soleil-Point
L1 : 1,481040e11 m.
Ce résultat correspond bien à celui que j'ai pu trouvé sur internet, en effet celle-ci
correspond à 1% de la distance Terre-Soleil, en considérant le x comme étant la distance
Terre-Point L1.
2014-2015 3/9

2) Calcul de la position du point de Lagrange L2
De même pour calculer la position du point L2, je ne m'occuperais que de la
résolution de son équation à l'équilibre, à savoir :
1 / (1 − x)² − u / x² + 1 − (1 + u)*x = 0
avec x = distance Soleil-Point L1 / distance Terre-Soleil
Pour résoudre cette équation j'ai donc utilisé la méthode de Newton-Raphson qui est
la plus approprié dans ce cas de figure.
Cette méthode est basé sur l’approximation du taux d’accroissement de f (une
fonction quelconque) par sa dérivée f' ' , f doit donc être dérivable sur le domaine de
recherche. On se rapproche du zéro en calculant par itérations successives x(i+1) = x(i) −
f(xi) / f '(xi) .
En reprenant le programme de simulation intitulé newtonRaphson.py, et en changeant
l'abscisse de départ par a = 1.001, je trouvais x=1,99 , or je sais que ce résultat est faux car
le point L2 n'est que le symétrique du point L1 par rapport à la Terre par conséquent x doit
être égal à x = 1,01. Après plusieurs vérifications de la dérivée et de la méthode, j'ai décidé
d'essayer de résoudre l'équation par la méthode de dichotomie utilisé pour le point L1.
L'intervalle fut ajusté pour 0,9 < x < 1,1 ,et le résultat obtenu fut x =1,897 j'en ai donc
conclu que soit l'équation devait être fausse ou soit que j'étais totalement dépourvus
d'intelligence. Après plusieurs essais infructueux mon programme affichait un problème de
'float', je l'ai donc mis en commentaire et ai décidé d'abandonner.
Néanmoins je vais considérer le point L2 comme étant situé à 1,01 fois la distance
Terre-soleil soit : 1,510e11 m , pour ne pas être bloqué par la suite.
3) Simulation de trajectoire
Définition des données :
–d : distance Soleil-Terre (on suppose que l’orbite terrestre est circulaire : R= cte =
149 600 000 000 m)
–r1 : distance Soleil-Point L1 (= 0,99*d m)
–r2 : distance Soleil-Point L2 (=1,01*d m)
–Ms : masse du Soleil (= 1,989E30 kg)
–Mt : masse de la Terre (= 5,972E24 kg)
–m : masse du satellite en kg
–G : constante gravitationnelle (= 6,67 10-11 Nm² / kg²)
2014-2015 4/9

–V : vitesse de rotation du satellite autour du Soleil (identique à celle de la Terre)
–A : accélération
a – Trajectoire de la Terre
On considère un système héliocentrique avec pour origine le Soleil
Bilan des forces agissant sur la Terre :
–Force d'attraction du Soleil : Fs = -(G*Ms*Mt / d**2)
En appliquant le principe fondamental de la dynamique sur la Terre, nous obtenons sur (er) :
Mt*A = - (G*Ms*Mt / d**2) (1)
A = - (G*Ms / d**2)
Pour nous simplifier la vie par la suite, nous allons nous placer dans un repère cartésien, ce
qui nous donne :
Ax = - (G*Ms / d**2)*cos(Ɵ) = (- G*Ms / d**2)*(x/d)
Ay = - (G*Ms / d**2)*sin(Ɵ) = (- G*Ms / d**2)*(y/d)
De plus nous connaissons les conditions initiales :
x[0] = d
y[0] = 0
Il ne reste plus qu'à calculer la vitesse, or étant donné que nous considérons une trajectoire
circulaire, nous pouvons affirmer que la vitesse est tangente en tout point au vecteur
d (selon er) :
A = - (G*Ms / d**2)
V²/d = -(G*Ms / d**2)
V = √(G*Ms / d)
Dont les conditions initiales sont :
Vx[0] = 0
Vy[0] = √(G*Ms / d)
2014-2015 5/9