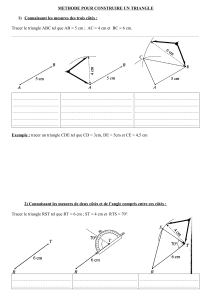
1°) Rappels. Exercice 1.1 Placer quatre points non alignés . Tracer

2FR – chapitre 5 – exercices
http://jouons-aux-mathematiques.fr MT FORCONI
1°) Rappels.
Exercice 1.1
Placer quatre points non alignés    .
Tracer  et .
Exercice 1.2
Tracer un triangle équilatéral  dont les côtés mesurent chacun 3cm.
Tracer la parallèle à  passant par , placer un point sur cette droite.
Tracer la perpendiculaire à  passant par .
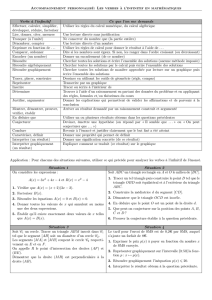
Exercice 1.3
On donne la représentation graphique suivante, dans laquelle  et
 sont deux carrés :
Complétez les propositions suivantes par le symbole signifiant « est
parallèle à » et le symbole signifiant « est perpendiculaire à ».
(AE)……(MF) (AM)……(LM) (EM)……(YZ)
(AI)……(AE) (AI)……(EM) (IE)……(LM)
Exercice 1.4
Tracer un triangle  suffisamment grand (un des côtés doit mesurer 12cm).
Mesurer les angles 
.
Faire le calcul :  
.
Mesurer l’angle 
 et comparer sa mesure avec le résultat du calcul précédent.
Exercice 1.5
Dans chaque cas, donner la nature de l’angle 
.
Exercice 1.6
a. Tracer un triangle  isocèle en  tel que   cm et   cm.
b. Tracer un triangle  rectangle en  tel que   cm et   cm.
c. Tracer un triangle  tel que   cm,   cm et 
.
d. Tracer un triangle  tel que   cm, 
 et  .
Exercice 1.7
a. Tracer un losange  dont les côtés mesurent 4cm et tel que   cm.
b. Tracer un rectangle  tel que la longueur mesure  cm et la largeur  cm.
c. Tracer un carré  tel que chaque côté mesure cm.

2FR – chapitre 5 – exercices
http://jouons-aux-mathematiques.fr MT FORCONI
2°) Médiatrice.
Exercice 2.1
Tracer un segment  de mesure 10 cm. Sur , placer un point  tel que   cm. Tracer la
médiatrice  du segment  et la médiatrice  du segment . Quelle hypothèse peut-on faire sur les
droites  et  ? Comment pourrait-on démontrer cette hypothèse ?
Exercice 2.2
Tracer un losange de centre .
1°) Démontrer que le triangle  est isocèle.
2°) Démontrer que  appartient à la médiatrice du segment .
3°) Démontrer que  appartient à la médiatrice du segment .
Exercice 2.3
Tracer un segment et sa médiatrice . On appellera  le milieu de . Placer un point  sur . Quelle
est la nature du triangle  ? Pourquoi ?
Placer un point  distinct de  sur  tel que  . Quelle est la nature du quadrilatère  ?
Pourquoi ?
Exercice 2.4
Tracez un triangle  tel que  cm,   cm et   cm.
Tracez avec précision la médiatrice de chacun des côtés du triangle. Qu’observez-vous ?
Tracez avec précision le cercle ayant pour centre le point d’intersection des médiatrices et passant par le
point . Qu’observez-vous ?
Remarque : cette propriété est vraie pour tous les triangles, ce cercle particulier s’appelle le cercle circonscrit
au triangle, et il a toujours pour centre le point d’intersection des médiatrices des côtés du triangle.
3°) Bissectrice.
Exercice 3.1
Tracer deux droites  et  sécantes en  formant un angle de mesure 75°. Tracer  la bissectrice
de l’angle 
. Tracer  la bissectrice de l’angle 
. Quelle hypothèse peut-on faire sur la position
relative des droites  et  ?
Exercice 3.2
Tracer un triangle  rectangle en  tel que   cm,   cm. Placer un point  distinct de  tel
que  soit un triangle rectangle en , avec   cm.
Citer la propriété du cours qui permet de démontrer que le point  appartient à la bissectrice de l’angle
.

2FR – chapitre 5 – exercices
http://jouons-aux-mathematiques.fr MT FORCONI
Exercice 3.3
Tracez un triangle  tel que  cm,   cm et   cm.
Tracez avec précision la bissectrice de chacun des angles au sommet du triangle. Qu’observez-vous ? On
appellera  le point d’intersection de ces bissectrices.
Tracez la perpendiculaire à  passant par . Elle coupe  en .
Tracez la perpendiculaire à  passant par . Elle coupe  en .
Tracez la perpendiculaire à  passant par . Elle coupe  en .
Tracez avec précision le cercle ayant pour centre le point  et passant par le point . Qu’observez-vous ?
Remarque : cette propriété est vraie pour tous les triangles, ce cercle particulier s’appelle le cercle inscrit au
triangle, et il a toujours pour centre le point d’intersection des bissectrices des côtés du triangle. On dit que
ce cercle est tangent à chacun des côtés du triangle.
4°) Cercles et disques.
Exercice 4.1
a. Rappeler la définition d’un cercle et celle d’un disque.
b. Pour chaque cas, préciser si on parle d’un cercle ou d’un disque.
i. Assiette plate
j. Equateur terrestre
k. Cerceau
l. Miroir circulaire
Exercice 4.2
Tracer un cercle de centre  et de rayon 2cm. Sur ce cercle, tracer :
i. Un rayon .
ii. Le diamètre .
iii. Une corde .
Exercice 4.3
Tracer deux points  et  distants de 3cm. Tracer le cercle de centre  et de rayon 2cm. Tracer le cercle de
centre  et de diamètre 5cm. Colorier en jaune la section du plan se trouvant à la fois dans le disque de
centre  et dans le disque de centre . Colorier en bleu la section du plan se trouvant dans le disque de
centre  mais pas dans le disque de centre .
Exercice 4.4
Placer un point . Tracer un arc de cercle de centre , de rayon 4cm, et ayant une ouverture de 50°.
Exercice 4.5
Placer un point . Tracer un arc de cercle de centre , de rayon 3cm, et ayant un angle au centre de 120°.
Exercice 4.6
La Terre a un rayon équatorial environ égal à 6 378 km. Calculer le périmètre de son équateur.

2FR – chapitre 5 – exercices
http://jouons-aux-mathematiques.fr MT FORCONI
Exercice 4.7
Deux petites fourmis ont inventé un super jeu pour les Jeux Olympiques des Fourmis. Une première fourmi,
qui aura un dossard jaune, devra parcourir le plus vite possible le périmètre d’un cercle de diamètre 1dm.
Pendant ce temps, une deuxième fourmi, qui aura un dossard vert, devra parcourir le périmètre d’un
rectangle dont les longueurs mesurent chacune 17cm et dont les largeurs mesurent chacune 15cm.
La fourmi qui gagne sera celle qui aura terminé son parcours en première.
Le Jury de la commission des Jeux Olympiques des Fourmis n’accepte pas le jeu : il pense que l’une des
deux fourmis serait avantagée. Laquelle ? Expliquer.