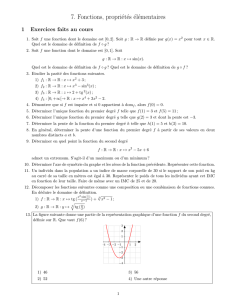
2013 fiche 16 calculer la pente dune droite fw

Lycée Paul Mélizan
14/12/13
Fiche 16
Calculer la pente d’une droite
Page 1 sur 1
F.W
Fiche 16 : Calculer la pente d’une droite
Pente d’une droite
La pente d’une droite est aussi appelée coefficient directeur de cette droite.
La pente d’une droite est la tangente de l’angle d’inclinaison de cette droite sur l’axe des abscisses.
Soit
BC
AC
ntcôtéadjace
côtéopposé
a tan
Calcul de la pente d’une droite
 Soit la droite passe par l’origine des axes
Après avoir tracé la droite, on constate qu’elle fait un angle α avec l’axe des abscisses, c’est l’angle
d’inclinaison de cette droite sur l’axe des abscisses. Son équation est du type y = ax.
y est l’ordonnée, x l’abscisse, a la pente de la droite ou coefficient directeur de la droite
On choisit sur celle-ci un point quelconque, autre que ceux utilisés pour la construire. Soit M ce point.
On relève sur la droite les coordonnées de ce point soit M (xM, yM).
On a la relation :
M
M
x
y
OH
OK
OH
MH
ntcôtéadjace
côtéopposé
a tan
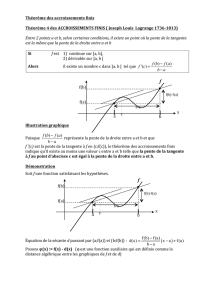
 Soit la droite ne passe pas par l’origine des axes
Après avoir tracé la droite, on constate qu’elle fait un angle α avec
l’axe des abscisses, c’est l’angle d’inclinaison de cette droite sur l’axe des abscisses. Son équation est du
type y = ax +b.
y est l’ordonnée, x l’abscisse, a la pente de la droite, b l’ordonnée à l’origine.
On choisit sur celle-ci deux points quelconques, autres que ceux utilisés pour la construire. Soient M et
P ces points. On relève sur la droite leurs coordonnées : soient M (xM, yM) et P (xP, yP).
On a la relation :
PM
PM xx yy
OHOH OKOK HH
KK
ntcôtéadjace
côtéopposé
a  '
'
'
'
tan
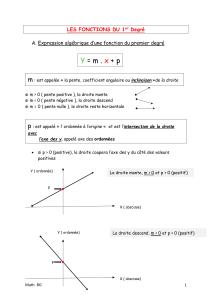
Hypoténuse : AB
α
Côté opposé à l’angle : AC
C
Côté adjacent à l’angle : BC
B
A