Texte - TACT

Découverte de la géométrie hyperbolique et de la géométrie elliptique à l’aide
de Cabri-géomètre
Marie-France Thibault
Marie-[email protected]
Département de mathématiques et d’informatique
Université du Québec à Trois-Rivières, Québec, Canada
Résumé : Ce texte permet de découvrir et de visualiser à l’aide du logiciel Cabri-géomètre les
principales propriétés de la géométrie hyperbolique et de la géométrie elliptique en deux
dimensions et de les comparer aux propriétés de la géométrie euclidienne du plan. Il contient
plusieurs figures Cabri qui permettent d’explorer ces différentes propriétés. Le lecteur est invité
à visualiser et à manipuler ces figures.
* Il est suggéré de maximiser la taille des figures pour voir les textes les accompagnant.

2
Les étudiants qui commencent leurs études universitaires n’ont pas toujours une vue très
structurée de la géométrie. Ils connaissent un certain nombre de résultats, mais ignorent souvent
comment les articuler les uns par rapport aux autres. Une partie de leurs connaissances est la
répétition de ce qu’on leur a dit, mais sans plus. Si on leur demande combien il y a de parallèles à
une droite donnée et passant par un point hors de cette droite, ils répondent «une», quelquefois
après hésitation, et si on leur demande pourquoi, ils ne savent pas toujours comment justifier leur
réponse. Souvent, ils n’ont entendu parler que de la géométrie euclidienne et n’imaginent pas que
d’autres géométries puissent exister.
Le logiciel Cabri-géomètre nous offre la possibilité de visualiser d’autres géométries et d’en
découvrir plusieurs propriétés. Cabri-géomètre permet ainsi de faire surgir la nécessité de preuves
ou de vérifications.
Je vous propose de découvrir et d’explorer la géométrie hyperbolique et la géométrie elliptique à
travers des modèles dans le plan euclidien.
Ce texte est accompagné d’un tableau en annexe, tableau qu’il peut être intéressant de remplir au
fur et à mesure de la lecture pour comparer les différentes propriétés que l’on découvrira au cours
de ce texte.
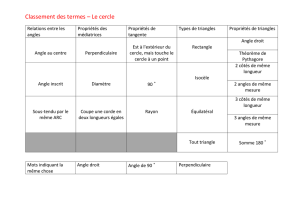
Droites et cercles
Qu’est-ce qu’une droite ?
Aucun étudiant ne peut vraiment répondre à cette question, à moins de dire que c’est une ligne
sans courbe, une ligne «droite». Ne nous étonnons pas. Même Euclide ne fut pas capable de le
formuler correctement. Il a dit qu’une droite était constituée de points et s’étendait indéfiniment.
Rien ne dit alors qu’une droite doit être «droite».
Pourquoi une «droite» ne pourrait-elle pas être un immense cercle, les sections que nous en
percevons nous semblant des «droites»? Semble-t-il que même les rayons laser courbent autour
de la terre et, donc, ne suivent pas notre idée intuitive d’un chemin droit. De plus, pourquoi

3
envisageons-nous le plan comme un immense carré ou rectangle dont les côtés sont infinis? Ne
pourrions-nous pas envisager le plan à partir d’un cercle de rayon infini ?
Drcercle.fig
Explorons donc des modèles de géométrie dans lesquels les «droites» pourraient être des «arcs de
cercle». Pour faire ceci, quels cercles pourraient être intéressants ? Une des premières règles de
la géométrie, appelées axiomes, demande que par deux points passe une et une seule droite. Or
par deux points passent plusieurs et même une infinité de cercles. Nous allons donc restreindre
les cercles étudiés.
Situons-nous à l’intérieur d’un cercle donné de rayon aussi grand que l’on désire, cercle que nous
appellerons cercle horizon, et considérons comme points de notre géométrie les points intérieurs
au cercle horizon. Il y a deux collections de cercles qui nous offrent l’existence et l’unicité
désirée pour les «droites».
♦ Par deux points intérieurs au cercle horizon, passe un et un seul cercle orthogonal au cercle
horizon, c’est-à-dire coupant le cercle horizon à angle droit.
♦ Par deux points intérieurs au cercle horizon, il y a un et un seul cercle passant par ces deux
points qui coupe le cercle horizon en un diamètre.
Cercint.fig
Nous avons donc ici deux modèles intéressants pour étudier la géométrie (ou différentes
géométries).
Modèle de Poincaré
À l’intérieur d’un cercle horizon, considérons, comme points, les points intérieurs au cercle
horizon et comme droites, la partie intérieure au cercle horizon des cercles orthogonaux au cercle

4
horizon. Seront aussi considérés comme droites les diamètres ouverts du cercle horizon, c’est-à-
dire les diamètres sans leurs extrémités.
Les commandes utiles pour les constructions dans le modèle de Poincaré sont fournies dans la
barre hyperbolique d’outils du logiciel Cabri-géomètre et sont préfixées par H (pour
hyperbolique). Les macro-constructions construites pour ce modèle à l’intérieur de cette
présentation seront préfixées par P.
Pmodele.fig
(suggestion : faire Revoir la construction)
Modèle de Klein
À l’intérieur d’un cercle horizon, considérons, comme points, les points intérieurs au cercle
horizon et les points du cercle horizon, les points antipodaux étant confondus, et comme droites,
la partie intérieure au cercle horizon des cercles coupant le cercle horizon en un diamètre, partie
intérieure à laquelle on ajoute le point d’intersection sur le cercle. Seront aussi considérés comme
droites les diamètres du cercle horizon augmenté de leur extrémité.
Comme ce modèle sera le seul modèle elliptique, les macro-constructions utiles pour travailler
dans ce modèle seront préfixées par E (pour elliptique).
Emodele.fig (suggestion : faire Revoir la construction)
Nous considérerons aussi un troisième modèle combinant notre idée intuitive de droite
euclidienne et de cercle horizon.
Modèle de Beltrami-Klein
À l’intérieur d’un cercle horizon, considérons comme points les points intérieurs au cercle
horizon et comme droites, la partie intérieure au cercle horizon des droites euclidiennes coupant
le cercle horizon.

5
BKmodele.fig (suggestion : faire Revoir la construction)
Nous comparerons les propriétés de ces modèles au modèle classique de la géométrie
euclidienne, c’est-à-dire le plan cartésien 2 R. Nous explorerons les propriétés des parallèles, des
perpendiculaires, la mesure des angles et des segments, les triangles semblables, les rectangles et
l’aire des triangles.
Parallèles
Une des grandes différences entre les modèles concerne l’existence et l’unicité des parallèles.
Quand deux droites sont-elles parallèles ? Dans le plan euclidien, deux droites sont parallèles si
elles sont équidistantes l’une de l’autre. Ceci fait appel à la notion de distance. Il y a une façon
beaucoup plus simple de cerner le parallélisme. Dans le plan euclidien, deux droites sont
équidistantes si et seulement si elles n’ont aucun point commun.
Définition : Deux droites seront dites parallèles si elles n’ont aucun point commun.
Combien y a-t-il de parallèles à une droite donnée et passant par un point donné? La propriété
euclidienne des parallèles est bien connue.
♦ Dans 2 R, pour toute droite m et tout point P hors de la droite, il existe une et une seule
parallèle à m et passant par P.
La propriété précédente étant la version moderne d’un des axiomes d’Euclide pour la géométrie
euclidienne, tout modèle la possédant est dit euclidien.
Les modèles de Poincaré, de Beltrami-Klein et de Klein ne partagent pas cette propriété comme
nous pouvons le découvrir dans les figures Cabri Pparal.fig, Bkparal.fig et Eparal.fig.
♦ Dans le modèle de Poincaré, pour toute droite m et tout point P hors de la droite, il existe une
infinité de droites parallèles à m et passant par le point P.