1Niv2 Géométrie ch 5

Mathématiques 1 Niv. 2 Deuxième partie GEOMETRIE
Collège Sismondi (S.Z., cours G.E.) 2007 - 2008 chap.5, p.1
CHAPITRE 5 :
CHAPITRE 5 :
TRIGONOMETRIE DU TRIANGLE RECTANGLE
TRIGONOMETRIE DU TRIANGLE RECTANGLE
§ 5.1 Mesures des angles
Comme objet géométrique, un angle est une partie (infinie) du plan, limitée par deux demi-droites issues
d'un même point. A cet objet géométrique, on peut attribuer une mesure de plusieurs façons différentes : on
peut le mesurer en degrés, en grades ou en radians.
Par définition, un degré est la mesure de la 90ème partie d'un angle droit.
C'est une mesure très ancienne : elle date des babyloniens et est sans doute en rapport avec le
nombre de jours de l'année officielle de cette époque, c’est-à-dire 360.
Par définition, un grade est la mesure de la 100ème partie d'un angle droit.
Cette mesure est récente ; c'est une tentative d'introduire le système décimal dans la mesure des
angles.
Mesurer un angle en degrés (ou en grades), consiste à "compter" combien de fois un angle de 1 degré (ou 1
grade) entre dans cet angle. Il s'agit donc de comparer un angle avec un autre considéré comme un étalon
de mesure.
La mesure d'un angle en radian est basée sur une autre idée.
Considérons un angle et des cercles centrés en son sommet :
L3
r1
L1
L2
r2
r3
Nous savons que le rapport entre le rayon d'un cercle et la longueur l'arc intercepté est constant
L1
r1
=
L2
r2
=
L3
r3
= …
(cela provient de la relation entre les angles, rayons, arcs de cercle et secteurs :
!
360
=
L
2!r
=
S
!r2
C'est ce rapport (constant pour un angle donné) que l'on appelle la mesure de l'angle en radian.
Cette façon de mesurer les angles en radians ne demande pas l'introduction d'une nouvelle unité, car les
radians sont obtenus comme un rapport entre deux longueurs ; les radians sont des grandeurs sans unité,
c’est-à-dire des nombres réels.
r
r
Par définition, un radian est la mesure d'un angle
qui intercepte un arc de cercle d'une longueur égale
à celle du rayon.

Mathématiques 1 Niv. 2
Deuxième partie GEOMETRIE
Collège Sismondi (S.Z., cours G.E.) 2007 - 2008 chap.5, p.2
Définition
Le cercle de rayon égal à 1 est appelé cercle trigonométrique
On sait que le périmètre d'un tel cercle vaut 2π.
Si le cercle utilisé pour mesurer un angle en radians est un cercle trigonométrique, alors la mesure de cet
angle s'obtient facilement car
L
r
=
L
1
= L.
Dans un cercle trigonométrique, la mesure d'un angle (en radians) est égale à la longueur
de l'arc intercepté.
Exemples
La mesure en radian d'un angle droit est égale au quart de la longueur du périmètre du cercle
trigonométrique, c’est-à-dire
2!
4
=
!
2
.
De la même façon, un angle plat mesure π en radians.
Les trois mesures d'angles, degrés, grades et radians, sont liées par la formule suivante :
![degré]
180[degré]
=
![grade]
200[grade]
=
![radian]
"[radian]
Cette formule exprime le fait que le rapport entre la mesure d'un angle et la mesure de l'angle plat est
toujours le même, quelque soit la mesure utilisée.
Exemple :
Si α = 90˚, alors
90˚
180˚
=
!
"
d'où, α =
90˚
180˚
π =
1
2
π =
!
2
Un angle droit mesure donc
!
2
radians.
Par la suite, nous n'utiliserons que les degrés et les radians.
Le tableau ci-dessous donne la correspondance entre des mesures d'angles en degrés et en radians.
Degrés
0˚
30˚
45˚
60˚
90˚
180˚
360˚
Radians
0
!
6
!
4
!
3
!
2
π
2π
Les calculatrices peuvent travailler avec des angles mesurés en degrés, en radians et en grades ; en
général, lorsqu'on met en marche une calculatrice, elle travaille en degrés et il faut changer le mode si l'on
veut travailler avec d'autres unités.
§5.2 Résolution de triangles rectangles
"Résoudre un triangle" signifie déterminer toutes ses grandeurs, ses trois côtés et ses trois angles,
connaissant la valeur de certains d'entre eux. Nous allons voir comment résoudre ce type de problème dans
le cas d'un triangle rectangle cette année, puis dans le cas général d'un triangle quelconque l’année
prochaine.

Mathématiques 1 Niv. 2
Deuxième partie GEOMETRIE
Collège Sismondi (S.Z., cours G.E.) 2007 - 2008 chap.5, p.3
Notations et vocabulaire concernant les triangles rectangles :
Dans le triangle ABC, rectangle en C, on note
habituellement a le côté BC, b le côté AC et c
l'hypoténuse (c’est-à-dire le côté AB).
De plus, et ceci dans le but de simplifier les
notations, a, b et c désigneront aussi bien les
segments BC, AC et AB que leurs longueurs, c’est-
à-dire les nombres réels
BC
,
AC
et
AB
.
Par rapport à l'angle α, a est le côté opposé et b le
côté adjacent.
A
B
C
a
b
c
!
"
Remarques
1. Si a est le côté opposé à l'angle α, il est le côté adjacent de l'angle β.
2. Un angle non-droit d'un triangle rectangle est délimité par deux côtés dont l'un est l'hypoténuse : on
peut donc parler sans ambiguïté du côté adjacent d'un angle non droit d'un triangle rectangle et nous
n'utiliserons les termes opposé et adjacent que par rapport aux angles non droits d'un triangle
rectangle.
3. Tous les triangles rectangles ayant un angle α commun sont semblables. Donc, on peut montrer que
les rapports
b
c
, respectivement
a
c
et
a
b
sont constants pour un angle α donné.
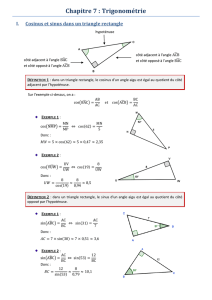
Définitions du cosinus, du sinus et de la tangente
Dans un triangle rectangle, on a les définitions suivantes (les justifications viendront en 2e année)
Le sinus de l’angle α (abrégé sin α) est le rapport entre les longueurs du côté opposé
et de l’hypoténuse
Le cosinus de l’angle α (abrégé cos α) est le rapport entre les longueurs du côté
adjacent et de l’hypoténuse
La tangente de l’angle α (abrégée tg α) est le rapport entre les longueurs des côtés
opposé et adjacent
côté adjacent à !
hypothénuse
!
côté opposé à !
cos α =
b
c
(
" côté adjacent "
" hypoténuse "
)
sin α =
a
c
(
" côté opposé "
" hypoténuse "
)
tg α =
a
b
(
" côté opposé "
" côté adjacent "
)

Mathématiques 1 Niv. 2
Deuxième partie GEOMETRIE
Collège Sismondi (S.Z., cours G.E.) 2007 - 2008 chap.5, p.4
Avec ces nouvelles définitions, valables seulement dans le cas d'un triangle rectangle, on peut facilement
trouver les valeurs manquantes d'un triangle dont on connaît au moins un côté et une autre donnée.
Exemples :
1. Si b = 34 et c = 53 , on trouve :
a =
b2+c2
=
342+532
=
3965
≈
62,96
tg(β) =
b
c
=
34
53
≈ 0,642.
d'où on tire β ≈ 32,68˚
γ = 90˚ – β = 90˚ - 32,68˚ = 57,32˚
A B
C
a
c
b
!
"
2. Si a = 50 et β = 40˚,
de cos(β) =
c
a
, on tire c = a·cos(β) = 50·cos(40˚) ≈ 38,30
de sin(β) =
b
a
, on tire b = a·sin(β) = 50·sin(40˚) ≈ 32,14
et encore γ = 90˚ – β = 90˚ – 40˚ = 50˚
3. Si l'on sait que l'angle que font des rayons solaires avec l'horizontale est de 60° et que l'ombre d'un
poteau mesure 6 m sur le sol, quelle est la hauteur h du poteau ? (on admet bien sûr que le poteau
est planté perpendiculairement au sol).
h
6
60°
tg 60° =
h
6
,
d'où
h = 6.tg 60° = 6.1,79 = 10,38 m
4. Projection orthogonale d'un segment sur une droite
La longueur p de la projection du segment de
longueur a sur une droite est déterminée par
p = a.cosα où α est l'angle formé par la droite
et le support des segments.
p
a
!
!