G9. Calculer un angle dans un triangle rectangle avec arccos.

Comment s’y prendre avec le arccosinus ?
Problématique !!
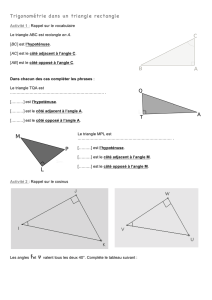
On sait qu’un triangle est rectangle et on connait deux de ses côtés.
La question est de calculer avec une précision d’ingénieur
(et non plus mesurer comme en 6ème ou 5ème, ce n’est plus assez précis)
la mesure de ses angles aigus.
Comment on fait pour trouver l’angle ?
Exemple expliqué.
Calcule, au degré près, la mesure de l’angle 
.
Il faut repérer l’hypoténuse et le côté adjacent de
l’angle qu’on cherche, ici l’angle 
.
L’hypoténuse, on l’a, elle est toujours en face l’angle droit, c’est PN.
Le côté adjacent à l’angle 
, c’est PA et on ne l’a pas !
Deux choix s’offrent alors à nous.
Côté adjacent (c’est quoi déjà ?).
Ça veut dire « Côté qui touche l’angle aigu mais qui n’est pas l’hypoténuse, sinon on l’appellerait par son nom ! »

Choix n°1 :
On calcule d’abord PA avec Pythagore 1.
Enfin, on tape à la calculatrice :
arccos (côté adjacent  Hypoténuse)
et on trouve la mesure de l’angle 
.
Bien préciser que le triangle est rectangle. Comme on l’a vu avec geogebra, la méthode ne s’applique
pas avec un triangle non rectangle.

Choix n°2 :
On fait le choix d’éviter Pythagore 1 en calculant l’autre angle, l’angle 
.
Côté adjacent à l’angle 
 Hypoténuse
Puis on termine par un calcul d’angle de 5ème.

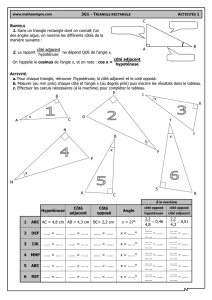
Exercice 1 :
Calculer les angles suivants :