Cosinus d’un angle aigu (trigonométrie) Exercices corrigés

Triangle rectangle et cosinus d’un angle aigu (trigonométrie) – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
1
Sont abordés dans cette fiche :
 Exercices 1 et 2 : calcul de la longueur d’un côté adjacent à un angle aigu
 Exercice 3 : calcul de la longueur de l’hypoténuse
 Exercice 4 : calcul du cosinus d’un angle et de la mesure de cet angle
 Exercice 5 : calcul du périmètre d’un rectangle
 Exercice 6 : calcul de l’aire d’un parallélogramme
Rappel : Cosinus d’un angle aigu
Dans un triangle rectangle,
 l’hypoténuse est le côté le plus long, opposé à l’angle
droit
 le côté adjacent à un angle aigu relie les sommets de
l’angle aigu d’une part et de l’angle droit d’autre part
 le cosinus d’un angle aigu est le quotient de la
longueur du côté adjacent à cet angle par la longueur
de l’hypoténuse
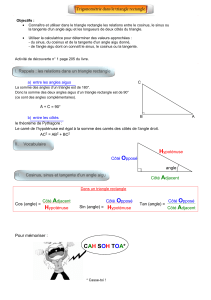
Exemple :
est un triangle rectangle en .
Le cosinus de l’angle aigu 
 est noté   et :
Le cosinus de l’angle aigu 
 est noté   et :
Cosinus d’un angle aigu (trigonométrie)
Exercices corrigés
angle droit
hypoténuse
côté adjacent à
l’angle aigu
sommet de
l’angle aigu
hypoténuse
côté adjacent à
l’angle aigu 
côté adjacent à
l’angle aigu 

Triangle rectangle et cosinus d’un angle aigu (trigonométrie) – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
2
 est un triangle rectangle en  tel que 
 et    cm. Calculer  en arrondissant le résultat
au millimètre près.
 1ère étape : On réalise une figure à taille réelle (ou en modifiant l’échelle) ou un schéma (à main levée)
en reportant les indications fournies par l’énoncé (codage).
 2ème étape : On s’assure que le triangle est rectangle (soit à l’aide de l’énoncé, soit à l’aide du codage de
la figure ou du schéma, soit en utilisant une démonstration).
D’après l’énoncé, le triangle  est rectangle en .
 3ème étape : On repère l’angle aigu, ainsi que l’hypoténuse et le côté adjacent à l’angle aigu.
 4ème étape : On écrit le cosinus de cet angle sous la forme d’un rapport de longueurs, en utilisant la
formule du cours.
 5ème étape : On cherche la valeur manquante de l’égalité.
Rappel : Produit en croix
Soient 4 nombres , ,  et , non nuls. En supposant que 
 , alors :
Exercice 1 (1 question) Niveau : facile
Correction de l’exercice 1
hypoténuse
côté adjacent à
l’angle aigu 
Ici, l’angle aigu à
repérer est l’angle
, indiqué en bleu.

Triangle rectangle et cosinus d’un angle aigu (trigonométrie) – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
3
Dans cet exercice, on cherche . A l’aide d’un produit en croix, on trouve que :
 6ème étape : On donne le résultat exact en remplaçant les longueurs et les angles connus par leurs
mesures respectives.
 7ème étape : On utilise la calculatrice pour trouver le résultat arrondi.
 8ème étape : On conclut.
Le segment  mesure  cm (valeur arrondie au millimètre près par défaut).
On donne la figure ci-contre. Calculer  et .
1) Calculons dans un premier temps .
D’après le codage de la figure, l’angle 
 est un angle droit.
Le triangle  est donc rectangle en .
Alors, dans le triangle  rectangle en , on a :
D’où, à l’aide d’un produit en croix puis en remplaçant par les mesures connues :
Le segment  mesure  (arrondi au centième par excès).
Remarque importante : Dans cet exercice, l’unité de longueur n’est pas précisée ; il ne faut donc pas écrire
d’unité après le résultat du calcul.
Exercice 2 (2 questions) Niveau : facile
Correction de l’exercice 2
Touches à saisir pour calculer cos 30
avec la Casio Collège 2D fx-92
avec la Texas Instrument TI-Collège

Triangle rectangle et cosinus d’un angle aigu (trigonométrie) – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
4
2) Calculons désormais .
Dans un triangle, la somme des angles est égale à  donc :
D’où : 
Dans le triangle  rectangle en , on a :
D’où, à l’aide d’un produit en croix puis en remplaçant par les mesures connues :
Le segment  mesure  (arrondi au centième par excès).
Remarque importante : On aurait pu également déterminer la distance  en utilisant le théorème de
Pythagore. En effet, le triangle  est rectangle en  donc, d’après le théorème de Pythagore, on à l’égalité
suivante :   , c’est-à-dire     . Enfin, il en résulte
que    . Le segment  mesure  (arrondi au centième par excès).
Rappel : Théorème de Pythagore
Si un triangle est rectangle, alors, d’après le théorème de Pythagore, le carré de la longueur de l’hypoténuse est
égal à la somme des carrés des longueurs des deux autres côtés du triangle.
Exemples :
Le triangle  est rectangle en 
donc, d’après le théorème de
Pythagore :     
Le triangle  est rectangle en 
donc, d’après le théorème de
Pythagore :     
Le triangle  est rectangle en 
donc, d’après le théorème de
Pythagore :   
Soit un cercle  de diamètre  et soit un point  du cercle tel que    cm et 
. Calculer la
mesure du diamètre du cercle .
Hypoténuse
Hypoténuse
Hypoténuse
Exercice 3 (1 question) Niveau : facile

Triangle rectangle et cosinus d’un angle aigu (trigonométrie) – Exercices corrigés
© SOS DEVOIRS CORRIGES (marque déposée)
5
Rappel : Triangle rectangle et cercle circonscrit
Si un triangle est inscrit dans un cercle qui a pour diamètre un de ses côtés, alors ce triangle est rectangle et a
pour hypoténuse le diamètre du cercle.
Le segment 
est un diamètre
du cercle
et  est un point
de ce cercle.
donc
Le triangle 
est rectangle
en  et a pour
hypoténuse
.
D’après l’énoncé,  est un cercle de diamètre  et   . Autrement dit, le triangle  est inscrit dans le
cercle , de diamètre . Par conséquent, le triangle  est rectangle en  et a pour hypoténuse .
Il en résulte que :
C’est-à-dire :
Le diamètre  du cercle  mesure exactement 6 cm.
Schéma :
On considère le schéma ci-contre. Les points ,  et  sont
alignés.
1) Calculer les valeurs arrondies au degré près de la
mesure de l’angle 
 et de la mesure de l’angle
.
2) En déduire que les droites  et  sont
perpendiculaires.
Correction de l’exercice 3
Exercice 4 (3 questions) Niveau : moyen