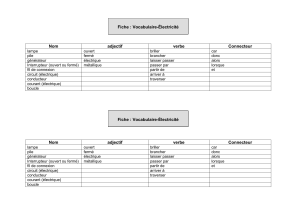
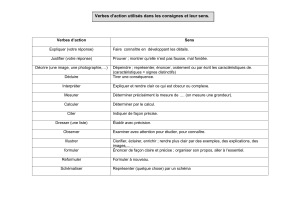
operateurs fermes correction

Opérateurs Fermés
(Correction )
1. Commençons par montrer que Im T=l2:Notons que
T x = (1x1;2x2;3x3; : : :) = (0;0;0; : : : ; )
si, et seulement si x= 0;ce qui prouve que Test injectif, par conséquent
l’inverse T1existe. Donc, il s’en suit que
T1(x1; x2; x3; : : :) = x1;1
2x2;1 3x3; : : :
alors
T1x 2=
+1
X
n=1
1
n2jxnj2
+1
X
n=1
jxnj2=kxk2;
iet T1est borné, 
T1 1.
De plus, comme
T1(1;0;0; : : : ; ) = (1;0;0; : : : ; );
on déduit que 
T1 = 1.
Comme T1est borné (i.e. T12BT1), il est en particulier un
opérateur fermé. Ceci signi…que le graphe GT1est un ensemble fermé.
Cependant, G(T)est obtenu à partir de GT1est en interchangeant
les cordonnées. Donc il s’en suit que le graphe G(T)est de Test aussi
fermé, et ainsi, nous avons montré que Test un opérateur fermé.
Notons cependant que Test un opéraeur non borné. En e¤et, il su¢ t de
voir que
kT enk=net kenk= 1:
2. Par dé…nition, T:D(T)!Hest fermé si le graphe
G(T) = f(x; y)2HH:x2D(T); y =T xg
est un ensemble fermé.
a) Soit A2B(H):Montrons que
G(T+A) = f(x; y)2HH:x2D(T); y =T x +Axg
est fermé. Il su¢ t de montrer que si (xn)D(T+A)et xn!xet
T xn+Axn!y; alors x2D(T+A)et (T+A)x=y:
Soit (xn)D(T+A) = D(T)et xn!xet T xn+Axn!y: Alors
T xn!ylim Axn=yAx:
Comme Test fermé, x2D(T)et T x =yAx; donc par réarrange-
ment, T x +Ax =y; et il s’en suit que T+Aest fermé.
1

b) En choisissant une suite (xn)D(T A)tel que
xn!xet T Axn!y:
Alors (Axn)D(T);et
Axn!Ax et T Axn!y:
En utilisant le fait que Test fermé, nous obtenons :
Ax 2D(T)
et
T Ax =y:
Cependant,
Ax 2D(T)signi…e que x2D(T A);
ce qui prouve que T A est fermé.
3. Il est clair que T:D(T)l2!l2est linéaire. De plus D(T)est dense
dans l2. En e¤et, l’ensemble de toutes les suites (xn);telle que, pour
certains N2N, nous avons xn= 0 pour n > N; est un sous ensemble de
D(T)et ce dernier sous ensemble est dense dans l2donc D(T)l’est aussi.
Soit x(n)D(T);et supposons que x(n)!x2l2et T x(n)!y2l2:
Si l’on écrit :
x(n)= (xn
1; xn 2; xn 3; : : :)et y= (y1; y2; y3; : : :);
alors
yT x(n)= (y1xn
2; y22xn 3; y33xn 4; : : :)!0dans l2:
En particulier,
xn
2!y1; xn 3!1
2y2; xn
4!1
3y3; : : : ; xn
k+1 !1
kyk; : : : ; pour n! 1;
donc la seule limite possible est :
x=lim xn
1;1
2y2;1 3y3; : : : ; 1 kyk; : : ::
Comme y2l2, il est évident que x2l2:En…n, il est trivial que T x =y;
donc x2D(T);et l’on a montrer que Test fermé.
4. Tétant un opérateur fermé, alors
x= lim un; un2D(T); et lim T un=z;
2

implique
x2D(T)et T x =z:
D’une manière similaire,
x= lim vn; vn2D(T); et lim T vn=q;
implique
x2D(T)et T x =q:
Maintenant, l’application est bien dé…nie (i.e. dé…nie d’une manière
unique), donc
lim
nT un=z=q= lim nT vn:
5. Voir le cours.
6. Soit (yn)T(A);et supposons que yn!y2H: Montrons que y2
T(A):
Comme yn2T(A);il existe au moins un xn2Atel que T xn=yn:
Choisisssons pour chaque ynun xn2Aayant cette propriété. Alors (xn)
dé…nie une suite sur un ensemble compact A. Donc (xn)contient une sous
suite convergente (zn)où zn!x2A: Nous avons donc montrer que
(zn)AD(T); zn!x2A et T zn!y2H:
Maintenant, T étant fermé, il s’en suit que x2D(T)et y2T(A):Ceci
montre que T(A)est fermé.
7. Il est clair que
ker T=fx2D(T) : T x = 0g
est un sous espace, donc il su¢ t de montrer qu’il est fermé.
Soit donc (xn)ker Tune suite telle que xn!x2H: Montrons que
x2ker T:
Comme Test fermé et que
T xn= 0 !0;
nous en déduisons que
x2D(T)et T x = lim
n!1T xn= 0:
Ce qui implique : x2ker T:
3