I - Notion d`angle A - Vocabulaire B - Notation II

CHAPITRE M1
ANGLES
I - Notion d'angle
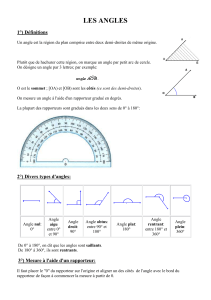
Un angle est une portion de plan délimitée par deux demi-droites ayant la même origine.
A - Vocabulaire
•Le point O est le sommet de l’angle.
•Les demi-droites [Ox) et [Oy) sont les côtés de l’angle.
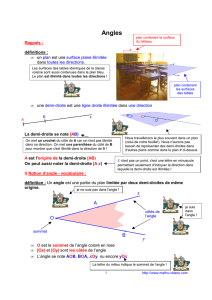
B - Notation
•Le secteur angulaire bleu est un angle saillant.
Il peut se noter de différentes manières (le plus souvent avec trois lettres,
celle du milieu étant toujours le sommet de l'angle) :
xOy
ou
yOx
ou
BOD
ou
DOB
ou
BO y
ou
yOB
ou
DO x
ou
xOD
.
•Le secteur angulaire rouge est un angle rentrant.
II - Utilisation du rapporteur
On peut mesurer l' « ouverture » d'un angle.
L'unité que l'on utilise au collège est le degré.
L'instrument qui permet de mesurer des angles est le rapporteur.
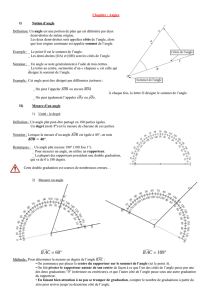
Voici un rapporteur gradué en degrés. Ce rapporteur a une
double graduation qui va de 0 à 180 degrés.
Attention : Cette double graduation est source de nombreuses
erreurs.
A - Pour mesurer un angle
On veut mesurer l'angle
CAB.
On place le centre du
rapporteur sur le sommet de
l'angle.
On place un zéro du rapporteur sur le côté [AC).
La mesure de l'angle est donnée par l'autre côté
de l'angle sur la même échelle de
graduation.
B - Pour tracer un angle de mesure donnée
Pour construire un angle
BUT
de
108°, on trace d'abord une
demi-droite [UB).
On place le centre du
rapporteur sur le point U. On
place un zéro du rapporteur
sur le côté [UB).
On marque, d'un petit trait-repère, 108°. On
trace la demi-droite d'origine U passant par le
repère. On place un point T sur cette
demi-droite.
O
B
D
x
y
C
A
B
centre A
B
C
On lit sur la même
graduation : 44°.
0 de la graduation extérieure
C
A
B
U
Bcentre U
B
0 de la graduation intérieure
On lit 108° sur la même
graduation, on affine avec
l'autre graduation.
T
U
B

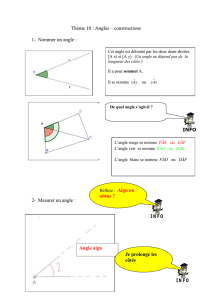
III - Différents types d'angles
On classe les angles par catégories selon leur mesure.
Angle Nul Aigu Droit Obtus Plat Rentrant Plein
Figure
Mesure 0° Entre 0°
et 90° 90° Entre 90° et 180° 180° Entre 180° et 360 ° 360°
Position
des côtés Confondus Perpendi- -culaires
Dans le
prolongement
l'un de l'autre
Confondus
Angles saillants
Soient A, B et C trois points distincts.
•Dire que « les droites (AB) et (AC) sont perpendiculaires » revient à dire que « l'angle
BAC
est un angle droit ».
•Dire que « les points A, B et C sont alignés » revient à dire que « l'angle
BAC
est soit nul, soit plat ».
Exemple :
JKL
JKM
MKL
 123°  57°  180° donc l'angle
JKL
est un angle plat et les points
J, K et L sont alignés.
IV - Bissectrice d'un angle
A - Définition
La bissectrice d'un angle est la demi-droite qui partage cet angle en deux angles de même mesure.
Exemple :
La demi-droite [UE) est la bissectrice de l'angle
SUA
.
B - Construction de la bissectrice d'un angle avec un rapporteur
Pour construire la bissectrice de
l'angle
MON
, on commence par le
mesurer à l'aide du rapporteur.
Il mesure 58°.
On prend la moitié de cette mesure
ce qui donne 29° et on fait un
trait-repère.
On trace la demi-droite d'origine O
passant par ce repère.
Cette demi-droite est la bissectrice
de l'angle
MON
.
Ox
@options;
@figure;
O = point( -1.73 , 2.37 ) { noir };
x = point( 3.07 , 2.37 ) { noir };
demiOx = demidroite( O , x )
{ noir };
y
Ox
y
Ox
y
Ox
y
Ox
@options;
@figure;
O = point( -1.73 , 2.37 ) { noir };
x = point( 3.07 , 2.37 ) { noir };
demiOx = demidroite( O , x )
{ noir };
yOx
y
Ox
@options;
@figure;
O = point( -1.73 , 2.37 ) { noir };
x = point( 3.07 , 2.37 ) { noir };
demiOx = demidroite( O , x )
{ noir };
y
M
57°
J
K L
123°
O
N
M
O
N
M
Bissectrice
de l'angle
O
N
M
U
S
AE
Bissectrice
de l'angle