integral

Int´egration et calcul de primitives
C. Ducourant
September 13, 2007
1 Int´egrale d’une fonction continue
•D´efinition :
Soit f une fonction d´efinie et continue sur un intervalle [a,b].
Le r´eel not´e Rb
af(x)dx est appell´e int´egrale de a `a b de f .
•Signe de l’int´egrale :
Soit f une fonction d´efinie et continue sur un intervalle I contenant les reels a et b tels que a≤b.
- Si f est positive sur [a,b], ⇒Rb
af(x)dx ≥0
- Si f est n´egative sur [a,b], ⇒Rb
af(x)dx ≤0
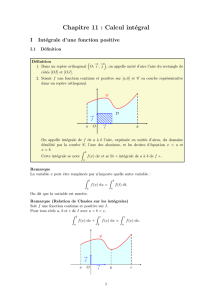
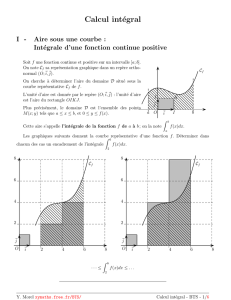
•Int´egrale et Aire :
Soit f une fonction d´efinie et continue sur un intervalle [a,b] et soit (Cf) sa courbe repr´esentative.
Soit (D), l’aire comprise entre l’axe des abscisses, la courbe (Cf) et les droites d’´equation x=a et
x=b.
•Si f est toujours positive sur [a,b] : Rb
af(x)dx =aire(D) (unit´es d’aire)
•Si f est toujours n´egative sur [a,b] : Rb
af(x)dx =−aire(D)
•Si f a un signe variable sur [a,b] : Rb
af(x)dx =aire(D1) −aire(D2) + aire(D3)
1

2 Propri´etes des int´egrale
•Relation de chasle :
Soit f une fonction d´efinie et continue sur un intervalle I. Pour tout r´eel a, b, et c de I :
Rb
af(x)dx +Rc bf(x)dx =Rc af(x)dx
•Lin´earit´e de l’int´egrale :
Soient f et g deux fonctions d´efinies et continues sur un intervalle I contenant a et b. Pour tous
r´eels αet βon a :
Rb
a[αf(x) + βg(x)]dx =αRc af(x)dx +βRc af(x)dx
3 Int´egrales et Primitives
•D´efinition d’une primitive :
Soit f une fonction d´efinie et continue sur un intervalle I. On appelle primitive de f sur I toute
application F d´erivable sur I telle que f soit l’application d´eriv´ee de F sur I.
F est primitive de f sur I ⇔ ∀x∈I, F 0(x) = f(x)
Par exemple:
F:x→x3est une primitive de f:x→3x2surR
Mais
G:x→x3−12 est aussi une primitive de f.
⇒on dit que F est une primitive de f sur ROn note l’ensemble des primitives de la fonction f : Rf(x)dx
Rf(x)dx =F(x) + C
En particulier :
R(ax +b)dx =1
aF(ax +b) + C
•Calcul d’une int´egrale `a l’aide d’une primitive :
Soit f une fonction d´efinie et continue sur un intervalle I et F une primitive de f sur I. Soient deux
r´eels a et b de I, alors:
Rb
af(x)dx = [F(x)]b
a=F(b)−F(a)
•Primitives classiques:
RPn(x) = Qn+1(x) + C, n est le degr´es du polynome Pn(x)
RPn(x)eax =Qn(x)eax +C
R[Asin(x) + Bcos(x)]ekxdx = [Dsin(x) + Ecos(x)]ekx +C
2

4 M´ethodes de calcul d’une int´egrale
•Int´egration par partie :
Soient u et v deux fonctions d´erivables sur un intervalle I telles que leurs d´eriv´ees u0et v0soient
continues sur I.
Pour tout r´eel a et b de I :
Rb
au0(x)v(x)dx = [u(x)v(x)]b
a−Rb
au(x)v0(x)dx
Par exemple :
Rb
axnekxdx = [ 1
kekxxn]b
a−1
kRb
anxn−1ekx...etc...
Rb
asin(x)ekxdx =1
1+k2[(ksinx −cosx)ekx]b
a
•D´ecomposition en ´elements simples :
Rx5
(x−3)(x+1)2=Pn(x) + C
(x−3) +D (x+1) +E
(x+1)2
avec n =diff´erence de degr´es entre num´erateur et d´enominateur, ici n=2. Si n´egatif alors pas
de polynome.
Exemple : Rb
a
1
(x−a)(x−b)=1
a−bR(1 x−a−1 x−b)dx
5 Int´egrales g´en´eralis´ees
Soit f une fonction d´efinie et continue sur un intervalle ouvert I, in´egrable sur tout segment contenu
dans I. On peut calculer l’int´egrale de f sur des segments de plus en plus grands , contenus dans
I, dont les bornes se rapprochent de celles de I. Quand l’int´egrale a une limite on dit qu’elle est
convergente, sinon on la dit divergente.
Par exemple :
R∞
af(x)dx =lim
B→∞ RB
af(x)dx
Ainsi pour k > 0 :
R∞
0e−kxdx =1
k
3

6 Tableau des d´eriv´ees usuelles
Figure 1: De Y. Villessuzanne - Bordeaux
4