R ρ ρ > 0 u

Faculté des Sciences 15 Septembre 2013
Département de Physique RATTRAPAGE : Physique 2 – STH
(Durée 1h)
Exercice 1:
Un cylindre de rayon R et de longueur infinie est uniformément chargé
en volume de densité ρ > 0 (Figure 1).
I – a) Déterminer le vecteur champ électrique ainsi que le potentiel en tout
point de l’espace. On prendra V = 0 pour r = R.
b) En déduire en tout point de l’espace le vecteur champ électrique créé
par un cylindre de rayon R0, de longueur infinie, uniformément chargé en
volume de densité - ρ < 0.
II - a) En utilisant le principe de superposition, déduire le champ électrique
créé par un cylindre creux de rayon intérieur R0 et extérieur R au point r tel
que R0 < r < R, de longueur infinie et uniformément chargé en volume de
densité ρ > 0. (figure 2)
b) Trouver la différence de potentielle V(R) - V(R0) entre les surfaces
intérieur et extérieur de ce cylindre.
Exercice 2 :
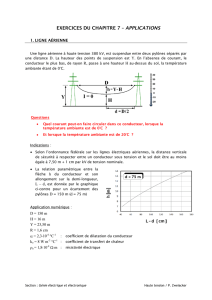
On considère le circuit électrique de la figure ci-contre.
On donne :
R1 = 2 Ω, R2 = 15 Ω, R3 = 10 Ω
I = 2 A, VA – VB = 9 V
Déterminer la valeur de la résistance R4
ur
r
ρ
R
Figure 1
Figure 2
ρ
ur
r
R0
R
E
R1
R2
R3
R4
I
I2
I3
I4
B
A
I1
E
F
C
D

Faculté des Sciences 15 Septembre 2013
Département de Physique
CORRIGE RATTRAPAGE : Physique 2 – STH
Exercice 1:
I – a) Symétrie cylindrique de la distribution de la charge  Pour toute surface fermée en forme de cylindre
de rayon r de longueur L, le champ électrique est radial et uniforme E = E(r).ur
Pour : r < R :
0
2
0
int L.r.
L.r.2.E
q
  E.dS
r.
2
)r(E 0
r
0.r.
2
)r( uE 
dV = - E(r).dr 
1
2
0Cr.
4
)r(V 
avec
0CR.
4
)R(V 1
2
0
2
0
1R.
4
C
et donc
)rR.(
4
)r(V 22
0
Pour r > R :
0
2
0
int L.R.
L.r.2.E
q
  E.dS
r
1
.
2R.
)r(E 0
2
r
0
2.
r
1
.
2R.
)r( uE 
dV = - E(r).dr 
2
0
2C)rln(.
2R.
)r(V 
avec
0C)Rln(.
2R.
)R(V 2
0
2
)Rln(
2R.
C0
2
2
et donc
r
R
ln.
2R
)r(V 0
2
b) Pour un cylindre de rayon R0 et de densité - les expressions du champ s’écrivent :
Pour : r < R0 :
r
0.r.
2
)r( uE 
Pour r > R0 :
r
0
2
0.
r
1
.
2
R.
)r( uE 
II - a) En utilisant le principe de superposition : dans la région R0 < r < R le champ est la résultante de deux
vecteurs en sens opposés :

r
2
0
0
r
0
2
0
r
0r
R
r
2
.
r
1
.
2
R.
.r.
2
)r( uuuE 
b) dV = - E(r).dr
dr.
r
R
r
2
dV R
R
2
0
0
R
R00  
 R
R
ln.R
2RR 2
rln.R
2
r
2
)R(V)R(V 0
2
0
2
0
2
0
R
R
2
0
2
0
0
0
Exercice 2 :
R1 = 2 Ω, R2 = 15 Ω, R3 = 10 Ω
I = 2 A, VA – VB = 9 V
VA –VB = R3.I3  I3 = 9/10 = 0.9 A
VA –VB = R2.I2  I2 = 9/15 = 0.6 A
I1 = I2 + I3 = 1.5 A
I = I1 + I4  I4 = 0.5 A
VA –VF = E = (VA –VB) + (VB –VF) = 9 + R1.I1= 12 V
VA –VF = R4.I4  R4 = 24 
E
R1
R2
R3
R4
I
I2
I3
I4
B
A
I1
E
F
C
D