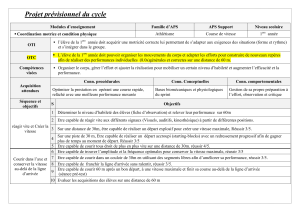
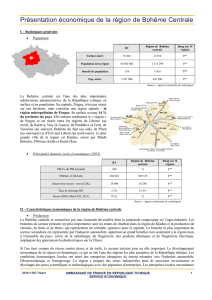
Chapitre : STATISTIQUES 1ere ES

Chapitre : STATISTIQUES 1ere ES
Exercice 1
Les 35 élèves d’une classe ont obtenu les notes suivantes à un test :
9 11 8 5 15 9 14
7 11 5 6 8 6 10
4 11 8 8 7 13 4
13 5 5 6 4 10 5
7 11 4 6 9 7 4
1) Donner la médiane et l’étendue de la série.
2) a) Si la plus haute note passe à 18, la médiane change-t-elle ?
b) On a oublié de noter une question aux 5 élèves qui ont 4. Si leur note passe à 6, la médiane change-t-
elle ?
c) On relève toutes les notes de 3 points. Quelle est la médiane ?
d) L’un des élèves qui a obtenu 7 est exclu de la série. Que devient la médiane ?
3) Déterminer l’écart interquartile de la série initiale.
4) Tracer la boîte à moustaches correspondante.
5) Déterminer la moyenne et l’écart-type de cette série.
Illustration
N= 35 x= 7.857143
Σx= 275.000000
Σx2= 2487.000000
V(x)=9.322449
σx= 3.053269
Min(x) = 4.000000
Q1(x)=5.000000
Med(x)=8.000000
Q3(x) = 10.000000
Max(x) = 15.000000
0 5 10 15 20
4 155 8.0 10
D. Le FUR 1/ ??

Chapitre : STATISTIQUES 1ere ES
Exercice 2
On donne la série des températures relevées à 8h du matin pendant 40 jours.
Températures en degrés xi-3 -1 2 4 9
Effectifs ni5 9 13 8 5
1) Soit S(x) = 5(x+ 3)2+ 9(x+ 1)2+ 13(x−2)2+ 8(x−4)2+ 5(x−9)2.
Développer, réduire et ordonner S(x)et montrer que S(x) = 40x2−158x+ 639.
2) Pour quelle valeur de xla somme S(x)est-elle minimum ? Justifier.
3) Soit E(x) = S(x)
Noù Nest le nombre de valeur de la série. Eest la dispersion moyenne des carrés des
écarts autour d’un nombre x. On sait que cette dispersion est minimale lorsque xest égal à la moyenne de
la série. De plus, le minimum est égal à la variance la série.
Retrouver alors à l’aide de ces résultats la moyenne et la variance.
Illustration
N= 40 x= 1.975000
Σx= 79.000000
Σx2= 4031.000000
V(x) = 12.074375
σx= 3.474820
Min(x) = −3.000000
Q1(x) = −1.000000
Med(x)=2.000000
Q3(x)=4.000000
Max(x)=9.000000
O
(CE)
A
−4−3−2−1 0 1 2 3 4 5 6 7 8
−10
0
10
20
30
40
50
60
70
D. Le FUR 2/ ??

Chapitre : STATISTIQUES 1ere ES
Exercice 3
Dans un groupe de 10 personnes, on mesure les tailles ti, en cm :
150 153 157 158 158 162 165 165 168 174
1) Donner la nouvelle série xi=ti−160 et la moyenne x.
2) Calculer la somme des carrés des xi, puis leur moyenne.
3) En déduire la variance Vde cette série xi.
Calculer l’écart-type σ.
NB : dans cet exercice, on détaillera les calculs que l’on fera sans utiliser les fonctions statistiques de la calculatrice.
Illustration
N= 10 x= 1.000000
Σx= 10.000000
Σx2= 480.000000
V(x) = 47.000000
σx= 6.855655
Min(x) = −10.000000
Q1(x) = −3.000000
Med(x)=0.000000
Q3(x)=5.000000
Max(x) = 14.000000
D. Le FUR 3/ ??

Chapitre : STATISTIQUES 1ere ES
Exercice 4
Soit la série suivante :
12 18 14 8 9 10 7 20 15 16 4
14 15 15 1 7 4 6 11 10 8 1
15 7 19 10 16 8 7 12 14 9 11
1) Déterminer la moyenne et l’écart-type de cette série.
2) Dessiner le diagramme en boîte de cette série.
3) Déterminer l’étendue et l’écart interquartile.
Illustration
N= 33 x= 10.696970
Σx= 353.000000
Σx2= 4535.000000
V(x) = 22.999082
σx= 4.795736
Min(x) = 1.000000
Q1(x)=7.000000
Med(x)=4.000000
Q3(x) = 15.000000
Max(x) = 20.000000
0 5 10 15 20
1 2074.0 15
D. Le FUR 4/ ??

Chapitre : STATISTIQUES 1ere ES
Exercice 5
Le tableau suivant donne la répartition (en %) des auditeurs d’une radio FM suivant leur âge.
âge [8 ; 13[ [13 ; 16[ [16 ; 18[ [18 ; 22[ [22 ; 27[
auditeurs 15 27 24 24 10
Après avoir effectué les calculs de densités, construire l’histogramme correspondant.
Illustration
6 8 10 12 14 16 18 20 22 24 26 28 30
2
D. Le FUR 5/ ??