intégration

Int´egration sur un segment
Quelques calculs d’aires :
Aire du rectangle l×L
Aire du parall´elogramme b×h
Aire du triangle B×h
2
Aire du disque de rayon r πr2
1 Primitives
1.1 D´efinition - Propri´et´es
D´ efinition
On dit que la fonction Fest une primitive de la fonction fsur l’intervalle I
si Fest d´erivable sur Iet si ∀x∈I , F ′(x) = f(x).
Exemple
F:x7→ x3
3+ 3 est une primitive sur Rde f:x7→ x2.
Exemple fondamental :
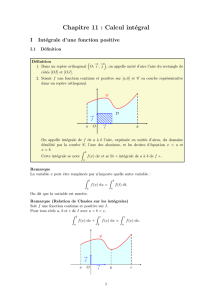
Soit fune fonction continue sur un intervalle [a, b] et Cfsa courbe dans un rep`ere orthonorm´e.
Pour simplifier, on se placera dans le cas o`u fest croissante et positive sur [a, b].
On note Ala fonction qui `a tout r´eel x∈[a, b] associe l’aire de la surface d´elimit´ee par Cfet l’axe des
abscisses, entre les abscisses aet x(On admet qu’elle est bien d´efinie sur [a, b]).
A(x)
ax x+h
f(x)
Cf
b
f(x+h)
Montrons que Aest d´erivable en tout x∈[a, b]
et que A′(x) = f(x)
c`ad que Aest une primitive de fsur [a, b].
Posons h > 0 : A(x+h)− A(x) est l’aire comprise entre les abscisses xet x+h.
Par croissance de f, cette aire est comprise entre le petit rectangle de hauteur f(x) et le grand rectangle
de hauteur f(x+h). D’o`u f(x)×h≤ A(x+h)− A(x)≤f(x+h)×h.
On en d´eduit que f(x)≤A(x+h)− A(x)
h≤f(x+h). Par continuit´e de f,f(x+h)−→
h→0f(x) et donc,
d’apr`es le th´eor`eme d’encadrement, le taux d’accroissement de Aadmet une limite `a droite en x
donc Aest d´erivable `a droite en xet A′
d(x) = f(x).
Par un raisonnement analogue quand h < 0, on obtient que Aest d´erivable `a gauche et que A′
g(x) = f(x).
Conclusion : Comme pour tout x∈[a, b]A′
d(x) = f(x) = A′
g(x),
Aest d´erivable en tout x∈[a, b] et A′(x) = f(x).
Remarque :A(a) = 0 ; en fait Aest l’unique primitive de fsur [a, b] qui s’annule en a.
Th´eor`eme
Toute fonction continue sur un intervalle Iposs`ede au moins une primitive sur I.
Th´eor`eme Soit Fune primitive de fsur l’intervalle I.
Alors l’ensemble des primitives de fsur Iest l’ensemble des fonctions de la forme F+ko`u k∈R.
D´emonstration
Soit k∈Ret G=F+k, alors G′=F′+ 0 = fdonc Gest bien une primitive de fsur I.
1

R´eciproquement, soit Gune primitive de fsur I. Alors F−Gest d´erivable sur Iet ∀x∈I, (F−G)′(x) =
F′(x)−G′(x) = f(x)−f(x) = 0 donc la fonction F−Gest constante sur I.
Donc, ∃k∈R/∀x∈I, F (x)−G(x) = k.
Th´eor`eme Soit fune fonction continue sur Iet x0∈I.
Alors pour tout y0∈R, il existe une unique primitive Fde ftelle que F(x0) = y0.
D´emonstration
L’existence est donn´ee par le th´eor`eme pr´ec´edent.
Montrons l’unicit´e : soient deux primitives Fet Gqui conviennent. On sait qu’il existe k∈R, tel que
F=G+k. Mais y0=F(x0) = G(y0) + k=y0+kimplique k= 0 et F=G.
Exemples
1. Chercher la primitive sur Rde f:x7→ x+ 1 qui s’annule en 1.
Une telle primitive est de la forme F:x7→ x2
2+x+k. Or F(1) = 0 ⇔k=−3 2. D’o`u l’unique
solution : x7→ x2
2+x−3 2.
2. Chercher la primitive sur R∗
+de g:x7→ 1
x2+ 3 qui s’annule en 2.
On trouve la fonction x7→ −1
x+ 3x−11 2.
1.2 Primitives de r´ef´erence
f(x)F(x) intervalle I
xn(n∈Z\{−1})xn+1
n+ 1 +CRsi n≥0, R∗
+ou R∗ −si n < 0
avec n=−2, 1
x2−1 x+CR∗
+ou R∗ −
xα(α∈R\{−1})xα+1
α+ 1 +CR∗
+
avec α=−1
2,1
√x2√x+CR∗
+
1
xln |x|+CR∗
+ou R∗ −
exex+CR
u′(x)(u(x))n(n∈Z\{−1})(u(x))n+1
n+ 1 +CI⊂ Duet si n < 0, une s’annulant pas
avec n=−2, u′
u2−1 u+Cune s’annulant pas sur I
u′uα(α∈R\{−1})uα+1
α+ 1 +Custrictement positive sur I
avec α=−1
2:u′
√u2√u+C u strictement positive sur I
u′
uln |u|+C u ne s’annulant pas sur I
u′eueu+C I ⊂ Du
On fera particuli`erement attention `a la valeur absolue pour la primitive de x7→ 1
x.
En effet, v´erifions que g:x7→ ln |x|est bien une primitive de x7→ 1
xsur R∗
−comme sur R∗ +:
si x∈R−∗,|x|=−xdonc g(x) = ln(−x) et g′(x) = −1
−x=1 x; et si x∈R+∗,g(x) = ln(x) d’o`u g′(x) = 1 x.
1.3 Op´erations sur les primitives
Proposition
Soient Fet Gdeux fonctions qui sont des primitives respectivement de fet de get soit λun nombre r´eel.
2

1. F+Gest une primitive de f+g,
2. λF est une primitive de λf.
D´emonstration
Par lin´earit´e de la d´erivation (F+g)′=F′+G′=f+get (λF )′=λF ′=λf.
2 Int´egration sur un segment
2.1 D´efinitions
D´ efinition
Soit fune fonction continue sur [a;b].On appelle int´egrale de a`a bde la fonction fle nombre r´eel
F(b)−F(a) o`u Fest une primitive quelconque de fet on le note Rb
af(t)dt.
Par convention, [F(t)]b
a=F(b)−F(a) et donc on a l’´ecriture suivante : Rb
af(t)dt = [F(t)]b
a=F(b)−F(a).
Exemple :R2
1x2dx = [x3
3]2
1=8
3−1 3=7 3.
Quel r´esultat aurait-on obtenu si on avait choisi la primitive x→x3
3+ 3 ?
Remarque
Le r´esultat ne d´epend pas de la primitive choisie ; en effet si l’on remplace la primitive Fpar une primitive
G, on sait qu’il existe k∈Rtel que G=F+k. Alors on a G(b)−G(a) = F(b)+k−(F(a)+k) = F(b)−F(a).
Th´eor`eme
Soit fune fonction continue sur un intervalle Iet x0∈Ialors la fonction F:x7→ Rx
x0f(t)dt est l’unique
primitive de fsur Iqui s’annule en x0. En particulier, Fest de classe C1sur Iet sa d´eriv´ee est F′=f.
Exemples
1. f:x7→ x+ 1 est continue sur Rdonc F:x7→ Rx
1(t+ 1)dt est l’unique primitive de fqui s’annule
en 1. Or F(x) = [t2
2+t]x
1=x2
2+x−(12 2+ 1) = x2 2+x−3 2. On retrouve bien le mˆeme r´esultat !
2. f:x7→ 1
xest continue sur ]0; +∞[ donc x7→ Rx
1
dt
test l’unique primitive de fsur ]0,+∞[ qui
s’annule en 1 : on la note ln. On obtient que ln est de classe C1sur ]0; +∞[ et (ln x)′=1
x.
.
2.2 Interpr´etation graphique
Exemple : soit fla fonction d´efinie sur [0,1] par f(x) = −3x+ 3.
Alors une primitive de fest F(x) = −3
2x2+ 3x. Donc R1
0f(t)dt =F(1) −F(0) = 3 −3/2 = 3/2.
Repr´esenter la fonction et calculer l’aire du triangle d´elimit´e par la
courbe de fsur [0,1] et les deux axes : on obtient 3/2.
Maintenant, consid`erons la fonction fsur [0,3] :
R3
0f(t)dt =F(3) −F(0) = −3/2∗9 + 3 ∗3 = −9/2.
Si on calcule l’aire des deux triangles du dessin : on obtient 3/2 et 6 ; on
remarque alors que 3/2−6 = −9/2.
C_f
1
3
1
3
0
Plus g´en´eralement, si a < b,Rb
af(t)dt repr´esente l’aire sign´ee du domaine d´elimit´e par C(courbe
repr´esentative de fdans un rep`ere orthonorm´e), l’axe des abscisses et les droites d’´equations x=a
et x=b.
3

a b
2.3 Propri´et´es g´en´erales de l’int´egrale
2.3.1 Premi`eres propri´et´es
Soit fune fonction continue sur un segment [a, b].
Les propri´et´es suivantes d´ecoulent de la d´efinition de l’int´egrale :
Za
a
f(t)dt = 0 Zb
a
f(t)dt =−Za
b
f(t)dt
En effet, si Fest une primitive de f, on sait que Ra
af(t)dt =F(a)−F(a) = 0 et
Ra
bf(t)dt =F(a)−F(b) = −(F(b)−F(a)) = −Rb
af(t)dt.
2.3.2 Relation de Chasles
Proposition
Soit fune fonction continue sur Iet soit a, b, c trois ´el´ements de Ialors on a
Zb
a
f(t)dt =Zc
a
f(t)dt +Zb
c
f(t)dt
2.3.3 Lin´earit´e de l’int´egrale
Proposition
Soient fet gdeux fonctions continues sur un segment [a, b] et λ∈R: alors
Zb
a
(f(t) + g(t))dt =Zb
a
f(t)dt +Zb
a
g(t)dt et Zb
a
λf(t)dt =λZb
a
f(t)dt.
2.3.4 Positivit´e et in´egalit´es
Proposition
Soient fet gdeux fonctions continues sur un segment [a, b] avec a≤b.
1. Si ∀t∈[a;b]f(t)≥0 alors Rb
af(t)dt ≥0
2. Si ∀t∈[a;b]f(t)≥g(t) alors Rb
af(t)dt ≥Rb
ag(t)dt
Remarque
Cette proposition signifie que l’on peut int´egrer des in´egalit´es, `a condition que les bornes de l’int´egrale
soient dans le bon sens : graphiquement, l’int´egrale ´etant repr´esent´ee par une aire, cette proposition est
´evidente.
Attention, si les bornes sont dans le mauvais sens, tout devient faux car
Ra
bf(t)dt ≥Ra
bg(t)dt ⇔ −Rb
af(t)dt ≥ −Rb
ag(t)dt ⇔Rb
af(t)dt ≤Rb
ag(t)dt !
D´emonstration 1.
Soit Fune primitive de f. Alors Fest d´erivable et F′=f≥0 par hypoth`ese, donc Fest croissante.
4

On en d´eduit que Rb
af(t)dt =F(b)−F(a)≥0 si a≤b.
Proposition
Soit fune fonction continue sur [a, b].
Si ∀t∈[a;b]f(t)≥0 et Rb
af(t)dt = 0 alors f(t) = 0 pour tout t∈[a;b].
5