Correction du contrôle n° 16 Exercice 1 R, S et U sont sur le cercle (C)

2010/2011
19 avril 2011 Correction du contrôle n° 16 3
ème
5
Exercice 1 (3 points)
R, S et U sont sur le cercle ( C ) de centre O.
Déterminer la mesure de l'angle ROU (en indiquant la propriété utilisée).
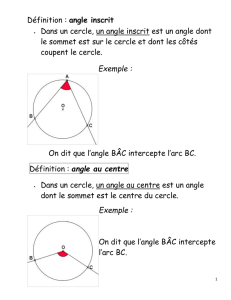
RSU est un angle inscrit dans le cercle. ROU est l’angle au centre
qui intercepte le même arc de cercle RU que RSU.
Or la mesure d’un angle inscrit est égale à la moitié de la mesure de
l’angle au centre qui intercepte le même arc.
Donc RSU = 1
2 ROU et ROU = 2 × RSU = 2 × 52
Finalement, ROU mesure 104°.
Exercice 2 (3 points)
Les points A, B, C et D sont sur le cercle ( C ).
Déterminer la mesure de l'angle CBD (en indiquant la
propriété utilisée).
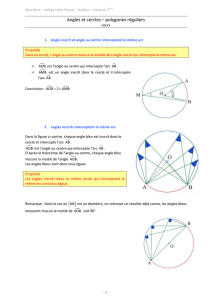
CAD et CBD sont deux angles inscrits dans le cercle qui
interceptent le même arc de cercle CD.
Or deux angles inscrits qui interceptent le même arc ont la
même mesure.
Donc CAD = CBD = 39°.
Exercice 3 (8 points)
La figure ci-contre est un pentagone régulier.
1. Déterminer la mesure de l’angle PZI.
PIOKA est un pentagone régulier. Donc tous les angles au
centre mesurent : 360 ÷ 5 = 72. Donc PZI mesure 72°
2. Déterminer la mesure de l’angle KPO.
KPO est un angle inscrit qui intercepte le même arc KO
que l’angle au centre KZO.
Or la mesure d’un angle inscrit est égale à la moitié de la
mesure de l’angle au centre qui intercepte le même arc.
Donc KPO = 1
2 KZO = 1 2 × 72 et KPO mesure 36°.
3. Déterminer la mesure de l’angle OKA
OKA est un angle inscrit qui intercepte le même grand arc OA que l’angle au centre OZA. De plus
OZA = 3×72 = 216°.
Or la mesure d’un angle inscrit est égale à la moitié de la mesure de l’angle au centre qui intercepte
le même arc.
Donc OZA = 1
2 OKA = 1 2 × 216 = 108 et OKA mesure 108°.

2010/2011
Autre façon
Le pentagone régulier est formé de 5 triangles isocèles semblables.
Le triangle ZOK est isocèle en Z. Ses angles à la base ont donc la même mesure.
Par conséquent OKZ = KOZ et OKZ + KOZ + OZK = 180. Donc OKZ = (180 – 72) ÷ 2 = 54°.
Finalement, OKA = 2 × OKZ = 2 × 54 et OKA mesure 108°.
Exercice 4 (5 points)
1. Construire au dos de cette feuille un hexagone régulier ABCDEF inscrit dans un cercle de
diamètre 10 cm.
2. Montrer que le triangle BDE est rectangle.
Je sais que le triangle BDE est inscrit dans le cercle et que l’un de ses côtés, [BE], est un diamètre
du cercle.
Or si un triangle est inscrit dans un cercle ayant pour diamètre l’un de ses côtés, alors ce triangle est
rectangle.
Donc le triangle BDE est rectangle.
3. Répondre à la question précédente en utilisant une autre méthode.
Je sais que BDE est un angle inscrit qui intercepte le même arc BE que l’angle au centre BOE (qui
mesure 180°).
Or la mesure d’un angle inscrit est égale à la moitié de la mesure de l’angle au centre qui intercepte
le même arc.
Donc BDE = 1
2 BOE = 1 2 × 180 = 90°.
Par conséquent, le triangle BDE est rectangle en D.