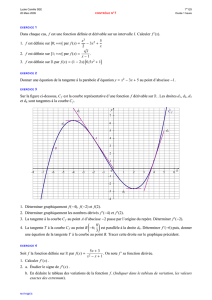
Partie III. LA G´EOM´ETRIE D`UNE FORME QUADRATIQUE

Partie III. LA G´ EOM´ ETRIE
D’UNE FORME
QUADRATIQUE, premier
´episode : LA CONIQUE
1

Introduction historique
La th´eorie des coniques a une histoire longue et riche et il faudrait un
volume entier pour l’´evoquer vraiment. Je me contenterai ici de citer quelques
faits parmi les plus saillants et quelques noms parmi les plus illustres.
En v´erit´e, une bonne partie de cette histoire est d´ej`a ´ecrite dans l’Anti-
quit´e. Pour les Grecs, les coniques sont, comme leur nom l’indique, les sec-
tions d’un cˆone `a base circulaire. Les historiens pensent g´en´eralement qu’il y
a eu un trait´e d’Arist´ee et Euclide sur le sujet, mais on n’en a nulle trace, si
bien que les deux noms essentiels que l’histoire a retenus pour la p´eriode de
l’Antiquit´e sont ceux d’Archim`ede et d’Apollonius.
Archim`ede (-287, -212) a surtout travaill´e sur les questions de mesure
(aires et volumes) des coniques et des quadriques. Il montre en particu-
lier le rapport de l’aire de l’ellipse et de son cercle directeur. L’un de ses
plus beaux r´esultats est la fameuse quadrature du segment de parabole 1
(qui requiert d’ailleurs de nombreux r´esultats auxiliaires sur celle-ci, sou-
vent prouv´es par des arguments m´ecaniques de leviers). Il ´etudie aussi les
sph´ero¨ıdes et cono¨ıdes (en langage moderne, les quadriques) et calcule cer-
tains volumes limit´es par ceux-ci.
Apollonius (-247, -170 ( ?)) a laiss´e un trait´e intitul´e Des coniques qui fait
le point des r´esultats connus `a son ´epoque, certains plus anciens et d’autres
originaux. C’est lui qui introduit le vocabulaire encore utilis´e `a l’heure ac-
tuelle (parabole, ellipse, hyperbole). Il ´etudie nombre de notions (tangentes,
asymptotes, diam`etres, axes, diam`etres conjugu´es, foyers, etc.), dont cer-
taines ´etaient peut-ˆetre connues avant lui. Il donne aussi, en substance, les
´equations de ces courbes : y=kx2pour la parabole, xy =kpour l’hyperbole,
x2/a2+y2/b2= 1 pour l’ellipse 2. On peut citer aussi un r´esultat qui pr´efigure
le th´eor`eme de B´ezout : Une section de cˆone ne coupe pas une section de cˆone
en plus de quatre points.
Il ne manque pas grand chose `a la th´eorie, sauf la d´efinition par foyer,
directrice et excentricit´e, qui est connue en tous cas de Pappus.
Bien que les Anciens aient d´ej`a en leur possession l’essentiel de la th´eorie,
les coniques vont faire l’objet d’une attention particuli`ere jusqu’au XX-i`eme
si`ecle. Il y a peu de math´ematiciens dont le nom ne soit attach´e, d’une
mani`ere ou d’une autre, `a la th´eorie des coniques. Il est donc hors de question
de les citer tous, mais il faut tout de mˆeme en mentionner quelques-uns. Au
1. Le mot parabole ne sera introduit que par Apollonius. Archim`ede parle de section
du cˆone droit rectangle.
2. Bien entendu, les choses ne sont pas dites ainsi. Par exemple, pour l’ellipse, il dit
Dans toute ellipse, la somme des carr´es de deux diam`etres conjugu´es quelconques est ´egale
`a la somme des carr´es des axes.
3

XVII-i`eme si`ecle on retiendra surtout les noms de Descartes (pour l’invention
de la g´eom´etrie analytique : les coniques de ce livre, comme on le verra, se-
ront avant tout donn´ees par des ´equations), de Pascal (pour son th´eor`eme sur
l’hexagone inscrit), de Desargues (pour l’involution associ´ee `a un faisceau) et
de Newton (pour la preuve de l’observation de Kepler 3sur les trajectoires des
plan`etes). Le rˆole de Newton ne se limite pas `a la loi de la gravitation univer-
selle. Une partie consid´erable de son œuvre traite directement de propri´et´es
g´eom´etriques des coniques (notamment sur les tangentes). On en verra un
petit aper¸cu au chapitre 3.
Au XIX-i`eme si`ecle, il faut ´evidemment commencer par Poncelet, inven-
teur des m´ethodes de g´eom´etrie projective qui sous-tendent ce livre, car c’est
avant tout aux coniques qu’il les applique. Nous verrons `a titre d’exemple, au
chapitre 3, un “lemme de Poncelet” o`u sont utilis´ees deux de ses m´ethodes
favorites : l’utilisation de la projection (ou de la transitivit´e) et le passage
par les complexes avec le principe de continuit´e. Poncelet obtient de nom-
breux r´esultats nouveaux, notamment deux th´eor`emes sur les tangentes et
surtout son fameux “porisme”, que nous ´etudierons au chapitre 4. ` A cˆot´e de
Poncelet, il faut se souvenir de Pl¨ucker (pour l’utilisation syst´ematique des
points cycliques), de Chasles (auteur d’un trait´e important sur le sujet et
`a qui l’on doit le calcul du nombre 4de coniques tangentes `a cinq coniques
donn´ees, sans doute le th´eor`eme le plus difficile sur les coniques), de Dandelin
et Qu´etelet (`a qui l’on doit la d´etermination des foyers d’une section conique)
et de Fr´egier 5, de Cayley (qui applique aux coniques sa colossale puissance
de calcul), j’en passe et de non moins illustres 6.
Signalons, plus pr`es de nous, qu’un grand math´ematicien comme Henri
Lebesgue n’a pas d´edaign´e d’´ecrire un trait´e sur les coniques 7.
En ce qui concerne les formes quadratiques, elles apparaissent avec les
´equations des coniques (donc au XVII-i`eme si`ecle). C’est Lagrange qui, le
3. Le rˆole de Kepler, s’il n’est pas essentiel d’un point de vue strictement math´ematique,
est cependant fondamental. En effet, c’est lui qui, en d´ecouvrant que les corps c´elestes
d´ecrivaient des coniques, a fait passer la th´eorie ´eth´er´ee des Grecs au statut de
math´ematiques appliqu´ees, ce qui nous vaut aujourd’hui les nombreux satellites artificiels
qui tournent autour de nos tˆetes.
4. Il y en a 3264.
5. Dont je ne sais pas grand chose, sinon qu’il ´etait professeur au coll`ege de Troyes et
ancien ´el`eve de l’´ecole polytechnique.
6. Jacobi, Steiner, Laguerre, etc.
7. Je ne r´esiste pas au plaisir de citer le d´ebut de la pr´eface de Paul Montel : Ce livre est
le premier ouvrage posthume d’Henri Lebesgue. L’auteur s’y retrouve tout entier. Dans son
attachement `a la G´eom´etrie d’abord : Lebesgue est avant tout un g´eom`etre et sa d´ecouverte
la plus ´eclatante, celle de l’int´egrale qui porte son nom, a une origine g´eom´etrique. On ne
saurait mieux dire.
4

premier, ´etablit en 1775 qu’une telle forme peut se d´ecomposer en somme
de carr´es de formes lin´eaires (cela revient `a l’existence d’une base orthogo-
nale) et Gauss utilisera beaucoup cette m´ethode, notamment dans la th´eorie
arithm´etique des formes binaires (ax2+bxy +cy2avec a, b, c entiers). Un
autre probl`eme provient de la th´eorie des coniques et des quadriques : la
recherche de leurs axes (dans un espace euclidien), ce qui revient `a la dia-
gonalisation des matrices sym´etriques. Ce probl`eme est abord´e par Euler et
surtout Cauchy. Citons enfin, vers 1850, les travaux de Jacobi et Sylvester
autour de l’invariance du rang et de la signature.
Le lecteur un peu g´eom`etre regardera avec un m´elange d’envie et d’effroi la
place que tenaient les coniques dans les manuels jusqu’au milieu du XX-i`eme
si`ecle (par exemple le livre de Deltheil et Caire [RD89b]). Il pourra peut-
ˆetre se dire que cette omnipr´esence ´etait un peu exag´er´ee ; il se dira surtout
que leur totale disparition dans les programmes actuels de l’enseignement
secondaire ou sup´erieur est d’une infinie tristesse.
5