Objectifs

3ème CHAPITRE 10: Géométrie dans l’espace.
Objectifs
Je dois savoir
Je dois connaître
Je fais le point
1.
… représenter en perspective une sphère et certains de ces
grands cercles
...calculer le volume d’une boule et l’aire d’une sphère
connaissant son rayon.
I. Sphère et Boule
- définition
- formules
P. 237 n°55, 56
P. 237 n° 57, 58
2.
… la nature des sections
- du cube ou du parallélépipède rectangle par un plan
parallèle à une face, à une arête ;
- du cylindre par un plan parallèle à la base ou
perpendiculaire à une arête ;
- de la pyramide ou du cône par un plan parallèle à la
base.
- d’une sphère par un plan.
II. Section d’un solide
par un plan.
p. 237 n° 59
3.
… calculer le rayon du cercle de section d’une sphère
par un plan. (connaissant le rayon de la sphère et la
distance du plan au centre de la sphère)
II. 3) section d’une
sphère et application
P. 237 n° 60
4.
… résoudre des problèmes, en particulier :
- calculs de longueurs et de volumes
- d’agrandissement et de réduction et de leurs effets
sur le volume.
P. 237 n° 61, 62, 63
Revoir aussi les volumes étudiés en 6ème, 5ème et 4ème ; Exercices en Autonomie p. 231
I. SPHERE ET BOULE
1) Définition
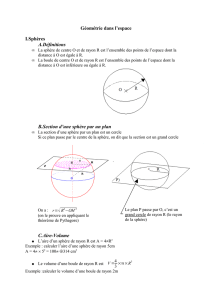
Une sphère a un centre O et un rayon R : si A est sur la sphère alors OA … …
La boule est l'intérieur de la sphère : si B est dans la boule alors OB … …
Un grand cercle est un cercle de centre O.
Pour donner l'impression de volume, on trace deux grands cercles à diamètres perpendiculaires, que l'on
représente par des ellipses.
2) Formules d’aire et de volume
L'aire de la sphère est : ………………………… Le volume de la boule est : ………………………………
Ex 1 : a) Calcule l'aire d'une sphère et le volume de la boule dont le rayon est 12 km.
b) Une sphère a une aire de 1 256 cm². Calcule le rayon de cette sphère puis le volume de la boule contenue dans
cette sphère.
Ex 2 : Le Culbuto est un jouet formé d'une demi-boule surmontée d'un cône comme l'indique
la figure ci-après. On donne AB = 10 cm et BC = 12 cm.
1) Calculer la distance AO.
2) Quel est le volume du jouet arrondi au cm3 près ?
xB
O
M
R
xA

D
C
A B
E F
G
H
N
II. SECTION D’UN SOLIDE PAR UN PLAN (VOIR P. 229)
Définition :
Exemple : Représenter en grandeur réelle la section du plan
et du pavé droit ci contre, sachant que AE = 6 cm, EF = 8 cm et EG = 5 cm.
1) Section de pyramide et de cône par un plan parallèle à la base :
Lorsque l’on coupe l’un de ces solides par un plan parallèle à la base, on fait
apparaître dans la partie supérieure un solide de même nature, et dans
la partie inférieure un tronc de pyramide ou un tronc de cône.
S, O, O’ sont alignés, S, A, A’ sont alignés, les droites (OA) et (O’A’) sont parallèles,
D’après ………………………………………………………………………… ,
on a : ………… = ………… = ………… = …
Conséquence : La section obtenue est une réduction de la base de la pyramide
ou du cône.
Si les dimensions d’un cône ou d’une pyramide sont multipliées par k, alors :
- les aires seront multipliées par ……
- les volumes seront multipliées par ……
2) Section d’une sphère
Ex 4 : La sphère a pour rayon OA = OB = 7cm et OH = 4cm.
1- Calcule, au cm3 près, le volume de la boule.
2- On réalise la section de cette sphère par un plan
a) Quelle est la nature de cette section ?……………………………
b) Calcule au dixième près le rayon de de cette section.
c) Calcule au dixième près l’aire de cette section.
d) Calcule le volume du cône de révolution engendré par la rotation du triangle OHA autour de [OB] ?
O
I
M
Si on coupe une sphère par un plan, le plan coupe la sphère en deux
parties. La partie supérieure s'appelle une calotte sphérique.
L'intersection est un cercle de centre I et de rayon r appelé petit cercle.
Le triangle IOM est rectangle en ……
D’après le théorème de Pythagore, on a :
...... = …… + ……
S
O
A
B
A'
O'
B'
Ex 3: La pyramide SOAB a pour base un triangle AOB rectangle en O. Elle est coupée
par un plan O’A’B’ parallèle à la base. On donne SA = 6m , SA’ = 4cm , SO = 4,5cm,
l’aire de OAB est 12m² et le volume de SOAB est 24m².
a) En justifiant, calcule la longueur SO’.
b) En déduire l’aire de O’A’B’ et le volume de SO’A’B’ à 10-2 près.
A
H
B
L’intersection d’un plan et d’un solide est appelée section
du solide par ce plan.
O

faces latérales
base
hauteur
3ème CHAPITRE 10: Géométrie dans l’espace. RAPPELS
Ex 1: Calcule le volume d'un pavé droit de hauteur est 3cm, de largeur 4cm et de longueur 7cm.
C) LE CYLINDRE
Un cylindre possède deux bases parallèles qui sont des disques de rayon R.
Le Volume du cylindre est : ………………………………………………………………
Ex 3: Calculer le volume d'un cylindre dont
la hauteur est 10cm et le diamètre de la base est 6cm.
D) LA PYRAMIDE ET LE CONE
Une pyramide est un volume dont les faces latérales
sont des triangles ayant un sommet en commun : le sommet de la pyramide.
La base de la pyramide est un polygone quelconque. O est le centre du polygone
Le triangle SAO est …………………………………………………
On peut appliquer
…………………………………………………………………………………………………
Le volume d’une pyramide est : …………………………………………………………………
Le volume d’un cône est : ………………………………………………………………
B
O
S
A
O
A) LE PAVE ET LE CUBE
Un pavé a … sommets, … faces et … arêtes.
Le volume du pavé est : ………………………………
L =
h
h
B) LE PRISME
Un prisme possède deux bases parallèles qui sont des polygones.
Le volume d'un prisme est …………………………………………
Ex 2: Calcule le volume d'un prisme dont la base est un triangle
rectangle de cotés de base 3cm, 4cm et 5 cm et de hauteur 3 cm.
génératrice
rayon
h
S
C
A
A
B
D
O
A

Ex4 : Le solide représenté ci-contre est constitué d'une pyramide régulière SABCD, de
sommet S, de base carrée ABCD et de hauteur [SO] et d'un pavé droit ABCDEFGH ; On
donne AB = 30cm, AE =10cm et SO = 30cm
1. Calculer le volume de la partie inférieure du solide.
2. Calculer le volume total du solide.
3. a) Calculer la valeur exacte de la génératrice SA.
b) En déduire la mesure, arrondie au degré, de l'angle
OAS ˆ
.
Ex 5 : Un réservoir d'eau est formé d'un cylindre et d'un cône.
1. Donne, en dm3, le volume exact de la partie cylindrique en fonction de 
2. Donne, en dm3, le volume exact de la partie conique en fonction de 
3. Donne le volume exact du réservoir, puis sa valeur arrondie à 1 dm3 près.
4. Ce réservoir peut-il contenir 1000 litres? Justifie la réponse.