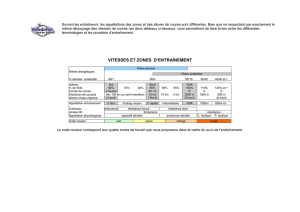
V - Activité d`enseignement et de recherche. Supports de cours à

1
M1 UE1 e3. Performance : de
l’athlète jusqu’au muscle
20h CM + 10h Tp
10 h CM. Modèles
mécaniques et énergétiques
de la performance humaine
http://robin.candau.free.fr [e-mail]
ECTS de l’enseignement : 3
1h CT : 2 questions parmi 10 (5 Perrey, 5 Candau) :
1. Applications d’un des modèle de type empirique sur des records actuels ou
des tests de terrain. Regard critique sur la formulation du modèle.
2. Concepts de résistance et d’endurance. Tests de terrain. Principe,
interprétations.
3. Principe du concept de vitesse critique et application dans une discipline
sportive de votre choix. Interprétation des deux paramètres obtenus.
Application dans le domaine de l’entraînement, du réentraînement ou de
l’EPS
4. Evaluation des aptitudes énergétiques à partir de performances sur différentes
distances. Principe du modèle de Péronnet et application sur des données
actuelles (records personnels ou records du monde)
5. Application du modèle d’Arsac et Locatelli (2002) à la performance en sprint
ou ½ fond. Limites et Perspectives.
Critères de notation
1. Qualité de la description des méthodes et du
principe du modèle cité
2. Qualité de la discussion et de l’interprétation des
résultats. Présence d’une application personnelle
dans le domaine de l’entraînement ou du
réentraînement
3. Qualité de l’expression, de la présentation des
graphiques
Travail personnel et logiciels
• Excel ou open office (gratuit)
• Madonna Berkeley (gratuit, www.berkeleymadonna.com/ )
• Scilab (gratuit, www.scilab.org), math lab
• Graph Pad, Sigma plot, Scientist, origin…
Modélisation des performances
humaines
2 objectifs :
• Mieux cerner les facteurs
mécaniques et énergétiques de la
performance humaine
• Applications dans le domaine de
l’entraînement, du réentraînement
ou de l’EPS
http://www.drawingsofleonardo.
Plan
1. Modèles empiriques
2. Modèles physiologiques

2
-
10
20
30
40
50
60
0 200000 400000 600000
t (s)
v (km/h)
Introduction
1. Décroissance non-linéaire des performances avec la durée de l’exercice
2. L’élite ne descend pas en dessous de 10 km/h => capacité énergétique pas
limitée
Quelle est la fonction
qui décrit le mieux
l’évolution des
performances en
fonction du temps de
course?
Records du monde
0
20
40
60
80
0 20000 40000 60000
Distance (m)
Vitesse (km/h)
Marche
Course
Patinage
Cyclisme
La diminution non-linéaire des performances est
retrouvée dans diverses locomotions
La relation devient linéaire avec la durée de l’exercice exprimée sur
une échelle logarithmique
Billat et al. Time in human endurance model Sports Med 1999 Jun; 27 (6): 359-379
200 m
800m
20 000m
1. Premières tentatives de description des
performances humaines
2. Concept de résistance
3. Concept d’endurance
4. Concept de limite pour l ’espèce humaine
5. Applications dans le domaine de
l ’entraînement
Modèles empiriques
I Modèles empiriques
• En 1906, Kennelly propose de décrire l ’évolution des
vitesses maintenues lors des records du monde en fonction de la durée
des épreuves (v/t) :
v = k tn(1)
k et n sont déterminées empiriquement
=> « loi de la fatigue » chez l ’homme et le cheval et pour
divers modes de locomotion
Kennelly AE. An approximate law of fatigue in the speeds of racing animals. Proc Am Acad Arts Sci 1906; 42 (15):
275-331
-
2
4
6
8
10
12
0 100000 200000 300000 400000 500000 600000
t (s)
v (m/s)
Test du modèle de Kennelly sur les records
du monde
• Surestimation à
partir du 200 km
• Erreur importante
Modèle de kennely 1906
v = k T
n
homme
k 13,90 variable
n 0,12 - variable
Erreur % 3% cellule cible
record du monde 97
6j
marathon
1997

3
Zoom sur l ’échelle de temps
Sous-estimation
Sur-estimation Description
grossière des
performances
=> les processus
énergétiques sous-
jacents sont plus
complexes et ne
peuvent pas être
décrit précisément
par cette simple
fonction
6
7
7
8
8
9
9
10
10
11
11
0 200 400 600 800 1000
t (s)
v (m/s)
Surestimation des performances
Du 800 au 3000 m
Principe de l’application du
modèle dans Excel
t (s) v réelle vmodèle (v réel - vmod)^2 Modèle de kennely 1906
9,84 10,16 11,97 3,25 v = k T
n
13,32 15,02 11,48 12,51
43,29 9,24 9,76 0,28 homme
101,73 7,86 8,68 0,67 k 16,38 variable
132,18 7,57 8,38 0,66 n 0,14 - variable
207,37 7,23 7,88 0,41 semc 21,54 cellule cible
224,39 7,17 7,79 0,38
284,88 7,02 7,54 0,27
440,67 6,81 7,10 0,09
764,39 6,54 6,58 0,00
1598,08 6,26 5,95 0,09
3415,6 5,86 5,36 0,24
3564 5,92 5,33 0,35
3600 5,86 5,32 0,29
4435,8 5,64 5,17 0,21
5358,1 5,60 5,04 0,31
7610 5,54 4,80 0,55
22220 4,50 4,15 0,12
59540 3,36 3,62 0,07
172800 2,62 3,13 0,26
518400 1,97 2,69 0,52
record du monde 97
-
2
4
6
8
10
12
14
16
0 100000 200000 300000 400000 500000 600000
t (s)
v (km/h)
Meade, 1956
reprend le modèle de Kennelly
et souligne le modeste pouvoir descriptif du modèle
La précision des mesures de performance lors des
records du monde doit permettre d ’identifier les
aptitudes énergétiques qui sous-tendent la
performance nécessité de formuler un modèle
approprié
Meade GP. Consistent running records. Science 1956; 124: 1025
Autres modèles empiriques
•1937, Grosse-Lordemann et Müller
log t = a • log P + b
en réarrangeant :
t = 10(a • log P + b)
a et b sont des constantes très variables d ’un sujet à
l ’autre sans signification biologique identifiée
•1943, Francis, modèle hyperbolique
(log d – 1.5) ×(v – 3.2) = 6.081
3,2 m/s = 11,5 km/h= vitesse qui peut être
maintenue théoriquement indéfiniment
=> 1ère suggestion d ’un modèle qui incorpore
l ’énergétique humaine
6 sujets sur
ergocycle, 6
exercices
épuisants
Ergocycle à friction sèche
Jauge de
contrainte
Capteur
de
vitesse
1. Premières tentatives de description des
performances humaines
2. Concept de résistance
3. Concept d’endurance
4. Concept de limite pour l ’espèce humaine
5. Applications dans le domaine de l ’entraînement
Modèles empiriques

4
• en 1860, le concept de résistance introduit par Henri et Farmer
Concept de résistance
(201 m)
(64 m)
Cet index de résistance reflétait fidèlement l ’état
d ’entraînement chez 18 étudiants en éducation physique
resistance
Concept de résistance et d’endurance
log t
P (w)
Tornvall G. Assessment of physical capabilities. Acta Physiol
Scand 1963; 58 Suppl.: 201
2 à 5 exercices épuisants
sur ergocycle avec 28
sujets
concept de résistance
introduit par Henri et
Farmer (1860)
V (km/h)
Effet de l ’entraînement sur
l ’endurance
Graig Virgin, champion du monde en 80
en 1972 -> f = 0.572
en 1976 -> f = 0.570
soit seulement 0.3% d ’augmentation de l ’endurance en 4
ans
(pas très surprenant ici chez un athlète d ’élite qui se maintient à son meilleur niveau)
L ’endurance ne s ’améliore pas ?
Evolution de l’endurance en fonction de l’âge
75
80
85
90
95
100
0 10 20 30 40 50 60 70 80
enfants âgés de 12 à 15 ans adultes
Tlim (min)
%VMA
Pourcentage de vitesse maximale aérobie pouvant être soutenu en
fonction de la durée de l'exercice pour des enfants et des adultes
(d'après Léger, 1996)
Adapté par Berthoin
L’endurance se bonifie avec les
processus de maturation
1. Premières tentatives de description des
performances humaines
2. Concept de résistance
3. Concept d’endurance
4. Concept de limite pour l ’espèce humaine
5. Applications dans le domaine de l ’entraînement
Modèles empiriques Concept de limite pour l ’espèce humaine
• En 1865, Henri barrière de 4’ au mile
sur la base d ’une analyse de l’évolution des
records du monde Mais dès 1954, Roger
Banister franchit cette barrière (3 ’59 ’ ’) !
• En 1954, Lietzke prévoit une vitesse max de
35.9 km/h (analyse des records du monde en
fonction du temps sur échelle log)
Mais v max est actuellement > 37 km/h sur
200m et > 40 km/h en vitesse de pointe

5
Atteinte d ’une limite pour l ’espèce humaine :
9’15’’ au 100m?
• Morton décrit l ’évolution des records du monde à travers
le siècle pour diverses distances particulières.
année
T100 m
Atteinte d ’une limite (?)
Fonction exp avec une
asymptote Analyse dépendante du contexte historique
et technologique
=> prédiction très incertaine car progrès
technologiques et dérives biologiques
difficilement prévisibles
9 ’15 ’’
Morton RH. The supreme runner: a theory of running and some
of his physiological attributes. Aust J Sci Med Sport 1984; 16:26-8
Limites pour l ’espèce humaine?
• 9’’15 au 100 m
• 3’04’’15 au 1500 m
• 23’40’’94 au 10 000 m
L ’athlète ultime possède (Keller, 1973) :
• une force maximale d ’accélération de
15 m.s-2.kg-1
• une VO2max de 154 mlO2/min/kg
• une capacité anaérobie de 140 ml/kg
Keller JB. A theory of competitive running. Physics Today 1973; 26: 42-7
Morton RH. The supreme runner: a theory of running and some
of his physiological attributes. Aust J SciMed Sport 1984; 16:26-8
Limites pour l ’espèce humaine?
• 9’’15 au 100 m
• 3’04’’15 au 1500 m
• 23’40’’94 au 10 000 m
L ’athlète ultime possède (Keller, 1973) :
• une force maximale d ’accélération de 15
m.s-2.kg-1
• une VO2max de 154 mlO2/min/kg
• une capacité anaérobie de 140 ml/kg
Keller JB. A theory of competitive running. Physics Today 1973; 26: 42-7
Morton RH. The supreme runner: a theory of running and some
of his physiological attributes. Aust J SciMed Sport 1984; 16:26-8
Valeurs actuelles
(41/3,6)/3 = 3,8 m.s-2.kg-1
85 mlO2/min/kg
100 mlO2/kg
9’’74
3’26’’
26’22’’
Les femmes vont-
elles courir plus vite le
marathon que les hommes?
• A partir d ’une augmentation fulgurante du record
féminin au marathon de 1980 - 1992, Whipp et
Ward ont prédit une vitesse supérieure pour les
femmes?
• Discipline olympique uniquement depuis 1984
=> nécessité de tenir compte du contexte historique
et social pour interpréter
Whipp BJ, Ward SA. Will women soon outrun men ? [letter] Nature 1992; 355: 25
1. Premières tentatives de description des
performances humaines
2. Concept de résistance
3. Concept d’endurance
4. Concept de limite pour l ’espèce humaine
5. Applications dans le domaine de l ’entraînement
– Orientation des athlètes en fonction de leur endurance
– Analyse de l’activité / détermination des points faibles et
forts de l’athlète
– Stratégie de course
Modèles empiriques Orientation des athlètes en fonction
de leur endurance
log t
V (min/mile)
concept de résistance Henri
et Farmer (1860)
7 min
Frederick et al., (1977)
Analyse statistique sur 62
internationaux en ½ fond et fond
•f = 1.0 ±0.09 pour le 1500m
•f = 0.699 ± 0.021 pour le 5000- 10 000m
•f = 0.619 ±0.02 pour le marathon
(endurance aptitude = à soutenir un haut
pourcentage de VO2max , index de Péronnet)