Mathenpoche4 : Cosinus d`un angle aigu Série1 : Prendre un bon

Mathenpoche4 : Cosinus d’un angle aigu
Série1 : Prendre un bon départ
Exo1 : Produits en croix
10q écrire le calcul qui permettrait de calculer la valeur du nombre inconnu x dans a = x/b ou b/x.
Exo2 : Démontrer qu’un triangle est rectangle
10q ordre aléatoire : 2q angles complémentaires, 1q parallèle à une perpendiculaire, 1q tangente, 3q réciproque
pythagore, 3q triangle dans cercle.
Exo3 : Reconnaître dans le triangle rectangle
10q é partir de triangles rectangles codés et représentés dans diverses dispositions, sélectionner l’hypoténuse ou
le côté adjacent à un angle donné ou l’angle dont le côté adjacent est donné (faire 3q sur l’hypoténuse et le reste
avec les histoire d’adjacent).
Exo4 : Nommer dans le triangle rectangle
Idem exo précédent, il ne s’agit plus de sélectionner mais de nommer, du style :
Le côté adjacent à l’angle aigu BAC est : […].
Exo5 : Nommer dans le triangle rectangle (bis)
Idem exo précédent mais plus à partir d’une figure codée mais à partir d’un texte décrivant la figure, du style :
ABC est un triangle rectangle en C, le côté adjacent à l’angle aigu BAC est : […].
A la validation montrer croquis « on est dans une configuration du type.
Exo6 : Synthèse pour le vocabulaire
Mélange des trois exos précédents mais dans des figures plus complexes : pour les cinq premières questions deux
triangles rectangles consécutifs, pour les cinq dernières un triangle rectangle+la hauteur issue de l’angle droit
tracée dedans.
S
M
R
U
R
S
T
H

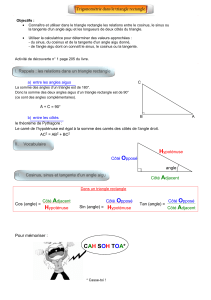
Série2 : Définition
Exo1 : Découverte
Conjecture en géométrie dynamique.
Q1 : Tracé de 2 demi-droites de même origine O puis un segment joignant les deux demi-droites et
perpendiculaire à l’une d’elle.
Q2 : Nommer l’hypoténuse et le côté adjacent à l’angle en O dans le triangle rectangle formé, à la validation
apparaissent la mesure de l’angle, les deux longueur et leur rapport.
Q3 tracé d’un autre segment perpendiculaire à l’autre demi-droite.
Q4 idem q2.
Q5 les deux segment deviennent mobiles perpendiculairement à leurs demi-droites respectives, l’angle entre les
deux demi-droites devient variable. On demande de déplacer les deux segments et d’observer le rapport puis de
faire varier l’angle et d’observer le rapport puis on demande si la valeur du rapport semble dépendre des
longueurs ou de l’angle.
Exo2 : Rapports égaux
Démonstration et lien avec le triangle rectangle.
Q1 dans ABC rectangle en B déplace B1 et C1 afin d’obtenir (B1C1)//(BC).
Au passage d’une bonne position l’angle droit formant le deuxième triangle rectangle apparaît.
Q2 Thalès à trous pour obtenir AB/AB1 = AC/AC1 (ou l’inverse)
Q3 obtention du rapport AB/AC = AB1/AC1 (mais pas l’inverse)
Q4 apparaît un deuxième segment [B2C2] et on demande de compléter l’égalité précédente par un troisième
rapport.
Q5 apparaît le codage de l’angle aigu en A, le prolongement en pointillés des demi-droites d’origine A et la
valeur approchée des trois rapports égaux. « On cherche à obtenir telle valeur numérique des trois rapports. Pour
cela essaie de déplacer [B1C1] ou [B2C2] puis [BC] et ensuite tu pourras essayer de faire varier la valeur de
l’angle aigu BAC » (à l’issue des deux premières manip apparaît le bouton permettant de faire varier cette
valeur).
Q6 « tu as constaté à la question précédente que la valeur commune des rapports AB/AC = AB1/AC1 =
AB2/AC2 ne dépend que de la mesure de l’angle aigu BAC. On note cette valeur cos BAC et on lit « cosinus de
l’angle BAC » » En faisant varier la mesure de l’angle BAC, propose un encadrement pour le nombre cos BAC.
A la validation montrer justification « ce nombre est le quotient de deux longueurs dont la plus grande est située
au dénominateur, donc ce nombre est bien compris entre 0 et 1. »
Q7 on montre une anim avec extraction d’un triangle rectangle de la figure
On explique que l’angle en R est le même que celui en A donc cosRST = cosBAC = …/…
Et on demande de compléter avec les lettres R, S et T.
Q8 lien avec le côté adjacent et l’hypoténuse du triangle RST.
Dans le triangle RST rectangle en T, [RS] représente … et [RT] …
Q9 dans un triangle rectangle le cosinus d’un des angles aigus est égal au quotient de la longueur du côté qui lui
est adjacent par celle de l’hypoténuse. (phrase à compléter à trou)
Q10 on montre un autre triangle rectangle EFG en F et on demande de compléter : le côté adjacent à l’angle en E
est […] et l’hypoténuse est […] donc cosEFG = coté adjacent à EFG/hypoténuse du triangle EFG = …/…
Exo3 : Ecrire la relation (assisté)
10q assistées à partir figure sur le modèle de la q10 de l’exo précédent, ie on demande d’identifier le côté
adjacent, l’hypoténuse et de compléter la formule.
Pour q7-8 et q9-10 on demande pour les deux angles aigus d’un même triangle.
A
B1
B2
B
C1
C2
C
A
B1
B2
B
C1
C2
C
R
T
S

Exo4 : Ecrire la relation
Idem exo précédent mais on demande juste de compléter la relation : dans le triangle ABC rectangle en B
cosBAC = …/…
Exo5 : Dans des figures complexes
10q Idem exo précédent mais figure complexe et l’élève doit préciser en plus dans quel triangle rectangle en quel
point. Pour les dernières questions on pourra lui demander d’écrire deux relations pour un même angle par
exemple dans le cas classique du triangle rectangle avec la hauteur issue de l’hypoténuse tracée.
Exo6 : Retrouver l’angle
10q (5q 1 seul triangle puis 5 plusieurs) on donne un rapport et il faut retrouver le nom de l’angle dont le rapport
donné est le cosinus. Dans les 5 premières questions en placer deux avec juste un texte, du style :
Dans le triangle ABC rectangle en C, BC/AB = cos ? (croquis à la validation).

Série 3 : Calculs
Exo1 : Calculer le cosinus d’un angle.
10q En utilisant la fonction cos de TA calculatrice réglée en « mode degrés », calcule la valeur du cosinus de
l’angle aigu en arrondissant comme demandé. Si tu n’as pas ta calculatrice utilise celle fournie par le logiciel.
cos 41° ≈ … (arrondir au dixième).
Demander des arrondis dixième, centième.
Exo2 : Calculer la mesure de l’angle.
10q En utilisant la fonction cos -1 de TA calculatrice réglée en « mode degrés », calcule la valeur de la mesure de
l’angle en arrondissant comme demandé.Si tu n’as pas ta calculatrice utilise celle fournie par le logiciel.
Si cos a = 0,985 alors a ≈ … (arrondir au dixième).
Demander arrondis à l’unité ou au dixième.
À partir de q5 proposer une valeur fractionnaire pour cos a, afin de vérifier que l’élève travaille à partir de la
valeur exacte (détecter ceux qui auraient utilisé la valeur approchée et faire une alerte spécifique).
Exo3 : Synthèse calculatrice.
En vrac sous la forme si a = 10° alors cos a ≈ … ou si cos a = 0,985 alors a ≈ …
On teste la bonne utilisation des fonctions cos ou cos –1.
Exo4 : Calcul de l’angle
5q sur le modèle suivant, pour les deux premières le texte de l’énoncé est accompagné d’une figure, pour les
trois suivantes non (un point d’interrogation l’invite à se réaliser un croquis et on lui montre un croquis à la
correction).
DEF est un triangle rectangle en E tel que
DE= 5 cm et DF= 9 cm.
Calculer la mesure de l’angle EDF.
cos ...... = ......
......
cos ...... = ......
......
angle EDF = ......
angle EDF ≈ .…....°
(arrondir au degré près)
Menus déroulants pour les étapes 1 et 3 et zones de saisie pour les étapes 2 et 4
Pour l’étape 3 proposer par exemple au choix cos –1 5/9 ou cos 5/9
Exo5 : Calcul du côté adjacent
Idem exo précédent mais pour le calcul de la longueur du côté adjacent :
RST est un triangle rectangle en T tel que
RS= 13 cm et angleSRT= 70°.
9
5
E
F
D
70°
13
R
T
S
(zones complétées
par les noms puis
par les valeurs)

Calculer la distance RT.
cos ...... = ......
......
cos ...... = ......
......
RT = ......
RT ≈ .…....
(arrondir au mm près)
Menus déroulants pour les étapes 1 et 3 et zones de saisie pour les étapes 2 et 4
Pour l’étape 3 proposer par exemple au choix 13 × cos70 ou 13 ÷ cos70 ou cos70 ÷ 13
Exo6 : Calcul de l’hypoténuse
Idem exo précédent mais pour le calcul de la longueur de l’hypoténuse :
IJK est un triangle rectangle en K tel que JK= 7,1
cm et angleIJK= 40°.
Calculer la distance IJ.
cos ...... = ......
......
cos ...... = ......
......
IJ ≈ ......
IJ ≈ .…....
(arrondir au mm près)
Exo7 : Synthèse
Reprise des 3 cas précédents sur 10q mais où on évalue plus le calcul intermédiaire, il y a juste deux étapes (la 1
et la 4) : une pour l’écriture de la relation avec des lettres (3 menus déroulants) et une zone de saisie pour le
résultat numérique.
Exo8 : figure complexe
L’élève doit préciser dans quel triangle rectangle il travaille, écrire la relation puis donner la valeur numérique
répondant à la question posée.
Dans le triangle … rectangle en … on a cos … = …/… donc … ≈ .…....
Exo9 : Calculs en deux temps
Q1 on demande le côté opposé et la résolution se fait à trous avec le calcul du complémentaire.
Q2 on donne l’opposé et l’adjacent et on demande un des angles aigu, la résolution se fait à trou avec calcul de
l’hypoténuse par Pythagore (s’arranger pour avoir une hypoténuse entière)
Q3 idem q1 mais on demande sèchement la réponse (on ne guide plus par le calcul du complémentaire).
Q4 idem q2 hypoténuse entière et on demande directement un des angles aigus
(zones complétées
par les noms puis
par les valeurs)
I
K
J
40°
7,1
(zones complétées
par les noms puis
par les valeurs)