Géométrie plane et Problèmes Activité 1 1

Géométrie plane et Problèmes
Activité 1
Carte de France : Coordonnées des villes.
1- Repère et coordonnées
1-1 Repère orthonormé
Un repère orthonormé est un ensemble de deux axes, (ox)et (oy), gradués avec la même unité
(Oi =Oj = 1 unité), perpendiculaires et ayant la même origine O.
(ox)⊥(oy)et (Oi =Oj = 1.
Définition 1.
Propriétés :
OIJ forme un triangle.
•Si le triangle Oij est rectangle isocèle en O, on définit un repère orthonormal (ou orthonormé).
•Si le triangle Oij est rectangle non isocèle, on parle de repère orthogonal.
•Si le triangle Oij n’est pas rectangle, on parle de repère quelconque.
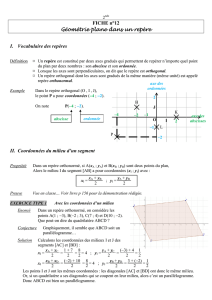
1-2 Coordonnées d’un point M
Propriétés :
Dans un repère orthonormé, tout point Mdu plan est repéré par : M(xM;yM).
•xMest l’abscisse de M.
•yMest l’ordonnée de M.
1-3 Distance entre deux points du plan
Activité 2
Trajet d’un véhicule : Algorithme pour déterminer une distance entre deux points.
Propriété :
Dans un repère orthonormé, la distance entre deux points A(xA;yA)et B(xB;yB)est :
AB =p(xB−xA)2+ (yB−yA)2.
∀M K 2nde
2016−2017 1/2ch3Géométrie plane

1-4 Milieu d’un segment
Propriété :
Dans un repère orthonormé, le milieu Idu segment [AB], deux points A(xA;yA)et B(xB;yB), a pour
coordonnées :
xI=xA+xB
2et yI=yA+yB 2.
1-5 Alignement de trois points
Pour déterminer l’alignement de trois points I,Jet K, on peut :
1. Définir la fonction affine fassociée à la droite (IJ);
2. Calculer f(xK)et conclure :
Si f(xK) = yKalors K∈(IJ)et donc les points I,Jet Ksont alignés,
sinon K6∈ (IJ)et donc les points I,Jet Kne sont pas alignés,
2 - Géométrie
2-1 Les triangles
Activité 2
C
O
A
B
Propriétés :
Les médiatrices des côtés d’un triangle sont con-
courantes au centre Ode son cercle
circonscrit.
C
G
AB
Les médianes d’un triangle sont
concourantes au centre de gravité Gdu
triangle.
C
H
A
B
Les hauteurs d’un triangle sont
concourantes en l’orthocentre Hdu triangle.
CI
AB
Les bissectrices des angles d’un triangle sont
concourantes au centre Ide son cercle inscrit.
2-2 Les quadrilatères
1. Si les segments [AC]et [BD]ont le même milieu, alors ABCD est un parallélogramme.
2. Si ABCD est un parallélogramme et ses diagonales sont isométriques, alors c’est un rectangle.
3. Si ABCD est un parallélogramme et deux côtés consécutifs sont isométriques, alors c’est un
losange.
4. Si ABCD est un losange et un rectangle, alors c’est un carré.
∀M K 2nde
2016−2017 2/2ch3Géométrie plane