I. Repère et coordonnées

Lycée Jules Verne 2016-2017
Seconde
Chapitre 3 - Repérage dans le
plan
A. Heliard
I. Repère et coordonnées
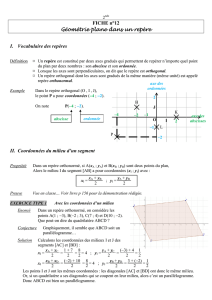
Définir un repère du plan, c’est choisir 3 points non alignés dans un ordre précis : O, I, J. On note ce repère
(O, I, J)et :
•le point Oest l’origine du repère ,
•la droite (OI)est l’axe des abscisses et le point Idonne l’unité sur cet axe,
•la droite (OJ)est l’axe des ordonnées et le point Jdonne l’unité sur cet axe.
Définition(s).
On distingue différents types de repères :
•Si le triangle OIJ est quelconque, le repère (O, I, J)est dit quelconque.
•Si le triangle OIJ est rectangle en O, le repère (O, I, J)est dit orthogonal. Dans ce cas, les axes du repère sont
perpendiculaires.
•Si le triangle OIJ est rectangle et isocèle en O, le repère (O, I, J)est dit orthonormé. Dans ce cas, les axes du
repère sont perpendiculaires et ont la même unité (OI =OJ).
Repère quelconque
O
J
I
Repère orthogonal
I
O
J
Repère orthonormé
O
J
I
Définition(s).
AB
C
M
NP
Q
Dans le triangle ABC, les points M, n et Psont les mi-
lieux respectifs des segments [AB],[AC]et [BC]. Le
point Qest le milieu du segment [MN ].
On se place dans le repère (A;B;C).
1. Lire les coordonnées des points A, B, C. puis cal-
culer les coordonnées des points M, N, P et Q.
2. Montrer que Qest le milieu du segment [AP ].
Exemple.
1

Lycée Jules Verne 2016-2017
Seconde
Chapitre 3 - Repérage dans le
plan
A. Heliard
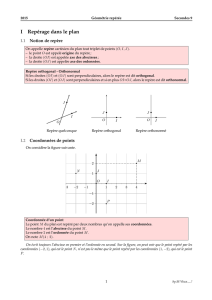
On considère un repère (O, I, J)du plan et un point quelconque M.
•En traçant la parallèle à (OJ )passant par M, on obtient sur l’axe (OI)l’abscisse xMdu point M.
•En traçant la parallèle à (OI)passant par M, on obtient sur l’axe (OJ )l’ordonnée yMdu point M.
•Le couple de réels (xM;yM)est le couple des coordonnées du point Mdans le repère (O, I, J).
Définition(s).
II. Coordonnées du milieu d’un segment
Dans le repère (O, I, J), on considère les points A(xA;yA)et B(xB;yB).
Alors le milieu Kdu segment [AB]a pour coordonnées
(xA+xB
2;yA+yB 2)
c’est à dire xK=xA+xB
2et yK=yA+yB 2.
Proposition.
On considère les points A(1; −2) et B(−3; 0). Calculer les coordonnées de Kmilieu du segment [AB].
Exemple.
☞ex 1, 3, 2 p 189
III. Distance entre deux points
Dans le repère orthonormé (O, I, J), on considère les points A(xA;yA)et B(xB;yB).
Alors
AB =p(xB−xA)2+ (yB−yA)2
Proposition.
On considère les points A(1; −2) et B(−3; 0). Calculer la distance AB.
Exemple.
☞ex 8, 9, 10 p 190
2

Lycée Jules Verne 2016-2017
Seconde
Chapitre 3 - Repérage dans le
plan
A. Heliard
IV. Rappels sur les configurations planes
1. Dans un triangle
•Un triangle isocèle possède deux côtés de même longueur et deux angles de même mesure.
•Un triangle équilatéral possède trois côtés de même longueur et trois angles de même mesure (60 degrés).
Définition(s).
Dans un triangle ABC quelconque :
1. La hauteur issue de A est la droite passant par A perpendiculaire à [BC].
Les trois hauteurs sont concourantes en l’orthocentre du triangle.
2. La médiane issue de A est la droite passant par A et le milieu du segment [BC].
Les trois médianes sont concourantes en le centre de gravité du triangle.
3. La bissectrice issue de A est la droite passant par A et divisant l’angle
\
BAC en deux angles égaux.
Les trois bissectrices sont concourantes en le centre du cercle inscrit au triangle.
4. La médiatrice du segment [BC]est la droite perpendiculaire au segment et passant par son milieu.
Les trois médiatrices d’un triangle sont concourantes en le centre du cercle circonscrit au triangle.
Proposition (Droites remarquables du triangle).
☞ex 41, 42, 43 p 199, 49 p 200
2. Dans un quadrilatère
1. Pour montrer qu’un quadrilatère est un parallélogramme, on montre une des propriétés :
•les diagonales se coupent en leur milieu
•les côtés opposés sont deux à deux de même longueur
•les côtés opposés sont deux à deux parallèles
2. Pour montrer qu’un quadrilatère est un rectangle, on montre que c’est un parallélogramme ET une des
propriétés :
•les diagonales sont de même longueur
•un des angles est un angle droit
3. Pour montrer qu’un quadrilatère est un losange, on montre que c’est un parallélogramme ET une des
propriétés :
•deux côtés consécutifs sont de même longueur
•les diagonales se coupent perpendiculairement
4. Pour montrer qu’un quadrilatère est un carré, on montre que c’est un parallélogramme ET un rectangle
ET un losange.
Proposition.
☞ex 51, 52, 54, 55, 56, 58 p 200-201
3