Devoir commun de mathématiques CORRECTION Exercice n°1

Devoir commun de mathématiques
CORRECTION
Exercice n°1 :
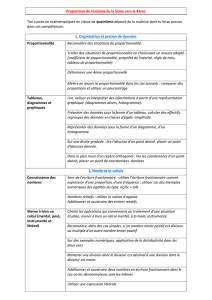
Pour chacune des propositions suivantes, déterminer la bonne réponse.
Propositions Réponse
Questions A B C D
1L'inverse de
7
est :
−7
−1
7
1
−7
1
7
D
2L'opposé de
5
est :
−0,2
−5
1
5
−1
7
B
3Deux nombres inverses ont
pour …
somme 1 produit 1 quotient 1 somme 0 B
4Deux nombres opposés ont
pour …
produit 0 somme 0 produit 1 somme 1 B
5Le produit de 8 nombres
tous négatifs est :
négatif égal à 0 positif On ne
peut pas
savoir
C
6La somme de 8 nombres
tous négatifs est :
négative égale à 0 positive On ne
peut pas
savoir
A
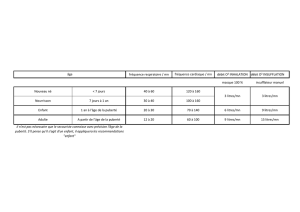
Exercice n°2 :
La distance de freinage
Df
exprimée en
m
d'un véhicule est donnée par la
formule :
Df=V²
254 f
où
V
est la vitesse du véhicule exprimée en
km/h
et
f
est
un coefficient qui dépend de l'état de la route.
a. Sur route sèche, on prendra
f=0,8
. Calculer la distance de freinage d'un véhicule
roulant à
50 km/h
.
Df=V²
254 f
=
502
254×0,8
=
2500
203,2
≈ 12,3 m
b. Sur route mouillée, on prendra
f=0,4
. Calculer la distance de freinage d'un
véhicule roulant à
50 km/h
.
Df=V²
254 f
=
502
254×0,4
=
2500
101,6
≈ 24,6 m
Exercice n°3 :
Soit un triangle
ABC
un triangle rectangle en
A
tel que
AB=8 cm
et
AC =6 cm
.
On appelle
M
le milieu de
[AB]
et
N
le milieu de
[AC ]
.
1. Construire le triangle
ABC
.

2. Déterminer la longueur
BC
. On arrondira au besoin au mm près.
Le triangle ABC est rectangle en A, il vérifie
l'égalité de Pythagore :
AB² + AC² = BC²
8² + 6² = BC²
64 + 36 = BC²
100 = BC²
BC =
√
100
= 10
Réponse : BC mesure 10 cm.
3. Démontrer que les droites
(MN )
et
(BC)
sont parallèles.
Je sais que : M est le milieu de [AB] et N le milieu de [AC]
or : « si une droite passe par les milieux des deux côtés d'un triangle alors elle est
parallèle au troisième côté .»
Donc : (MN) // BC
Exercice n°4 :
Voici un relevé des températures
T
minimales en degrés Celsius dans une
base du Pôle Nord sur une semaine de janvier :
Jour Lundi Mardi Mercredi Jeudi Vendredi Samedi Dimanche Moy.
T ( en °C) -23 -31 -28 -25 -19 -22 -20 -24
1. Calculer la température minimale moyenne de cette semaine.
Rappel : La moyenne s'obtient en additionnant toutes les valeurs et en divisant par le
nombre de valeurs.
−23+(−31)+(−28)+(−25)+(−19)+(−22)+(−20)
7
= -24
Réponse : la moyenne minimale de cette semaine s'élève à -24°C
2. Cette moyenne est deux fois plus petite que celle d'une semaine du mois de mai.
Quelle est donc la température minimale moyenne d'une semaine du mois de mai ?
−24
2
= -12
Réponse : la température minimale
moyenne d'une semaine du mois de mai est
-12°C
Exercice n°5 :
1. Expliquer pourquoi le volume de glace
est proportionnel au volume d’eau liquide.
Cette situation est une situation de
proportionnalité car sa représentation
graphique est une droite passant par
l'origine.
AB
C
N
M

2. Compléter la colonne grisée du tableau ci-dessous en faisant apparaître les traits de
lecture sur le graphique.
Volume d’eau
liquide (en L) 10 28 b
Volume de glace
(en L) 11 a 143
3. Compléter alors par le calcul les deux dernières colonnes du tableau en faisant
apparaître clairement votre démarche.
1ère possibilité : calcul du coefficient de proportionnalité :
Appelons k le coefficient de proportionnalité : k =
11
10
= 1,1
Calcul de a:
a = 28 x 1,1 = 30,8
Réponse : le volume de glace
correspondant à 28 litres d'eau est 30,8
litres.
Calcul de b :
b = 143 ÷ 11 = 130
Réponse : le volume d'eau correspondant
à 143 litres de glace est 130 litres.
2ème possibilité : calcul de la quatrième proportionnelle :
a =
11×28
10
=
308
10
= 30,8
Réponse : le volume de glace
correspondant à 28 litres d'eau est 30,8
litres.
b =
10×143
11
=
1430
11
= 130
Réponse : le volume d'eau correspondant
à 143 litres de glace est 130 litres.