Feuille de TD1 1 Entiers naturels et récurrence

Institut galil´ ee
Math´ ematiques pour l’Informatique 2016 Janvier 2016
Sylviane R. Schwer
Feuille de TD1
1 Entiers naturels et r´ecurrence
Exercice 1 Etudier la d´emonstration suivante, qui prouve que deux nombres quelconques
sont ´egaux :
Soient trois nombres a,bet cstrictement positifs tels que a=b+c.
a=b+c⇔a(a−b)=(b+c)(a−b),
d’o`u a2−ab =ab+ac−b2−bc ⇔a2−ab−ac =ab+ac−b2−bc−ac ⇔a(a−b−c) = b(a−b−c),
En simplifiant par a−b−c, on obtient a=b.
Exercice 2 On d´efinit la fonction d’Ackermann1A:N2→Npar r´ecursion de la mani`ere
suivante:
(i)A(0, y) := y+ 1
(ii)A(x, 0) := A(x−1,1) pour x > 0
(iii)A(x, y) := A(x−1, A(x, y −1)) pour x > 0, y > 0.
1. Montrer que ∀y∈N,A(1, y) = y+ 2
2. Montrer que ∀y∈N,A(2, y)=2y+ 3
3. Montrer que ∀y∈N,A(3, y)=2y+3 −3
4. Montrer que ∀y∈N,A(4, y)=2∧∧(y+ 3) −3.
a∧∧best la notation de Donald Knuth pour repr´esenter aa
.
.
.
a
, avec boccurrences de
a.a∧∧1 = a;a∧∧ 2 = aa;a∧∧(n+ 1) = aa∧∧ n
Calculer A(4,1) et A(4,2).
5. Montrer que la fonction d’Ackerman est bien calculable sur N×N, c’est-`a-dire que
pour tout couple d’entiers (x,y), le calcul de A(x, y) est effectif.
Exercice 3 Le paradoxe du chauve2. On arrache un cheveu `a la tˆete d’un homme chevelu.
Celui-ci est-il devenu chauve ? Evidemment non. Puis on lui arrache un second cheveu,
est-il devenu chauve ? et trois ? . . . , et n ?
1La fonction d’Ackermann est un exemple simple de fonction r´ecursive non primitive r´ecursive.
L’ensemble des fonctions primitives r´ecursives contient les fonctions constantes, les projections, la fonc-
tion successeur et est clos par composition et par r´ecursion primitive : f(x1,· · · , xp,0) = g(x1,· · · , xp)et
f(x1,· · · , xp, n + 1) = h(x1,· · · , xp, n, f (x1,· · · , xp, n)), avec get hprimitives r´ecursives. les fonctions
arithm´etiques ´el´ementaires, les fonctions puissances, factorielles sont primitives r´ecursives. Les fonctions
r´ecursives sont toutes les fonctions calculables par un ordinateur.
2Paradoxe produit par le M´egarite Eubulide de Milet, au IV◦si`ecle avant l’EC. Ce type de paradoxe
est appel´e sorite.
1

Montrer que l’application du principe de r´ecurrence conduit `a prouver qu’un homme
chauve n’est pas chauve. O`u r´eside le paradoxe ?
Produire un paradoxe similaire qui prouve qu’un riche n’est pas riche.
Exercice 4 Etudier la d´emonstration suivante, d´eriv´ee d’un paradoxe propos´e par le
math´ematicien et logicien Alfred Tarski.
Supposons que pour tout paquet Pnde ncrayons, nous voulons d´emontrer la proposition
suivante :
(p∈Pnet q∈Pn)⇒(p et q ont mˆeme couleur)
Cette implication est vraie pour n=1.
Supposons qu’elle est vraie pour n, prouvons la pour n+ 1
Soit Pn+1 un ensemble de n+1 crayons not´es p1,···pn, pn+1. Notons Pnle paquet constitu´e
des ncrayons p1,···pnet Qnle paquet constitu´e des ncrayons p2, p3···pn+1.
D’apr`es l’hypoth`ese de r´ecurrence, d’une part p1=p2=··· =pnet d’autre part p2=
p3=··· =pn=pn+1, ce qui d´emontre le th´eor`eme par r´ecurrence.
2 relations d’´equivalence
Exercice 5 (Pour chacune des relations, ´etudier si c’est une une relation d’´equivalence?
Si oui, quelles en sont ses classes ?
1. Dans l’ensemble des droites du plan, la relation ˆetre perpendiculaires ?
2. Dans l’ensemble des droites du plan, la relation ˆetre parall`eles ?
3. Dans l’ensemble des droites du plan, la relation ˆetre concourantes ?
4. Dans R∗, la relation αd´efinie par uαv ⇐⇒ u×v > 0.
5. Dans C, la relation d´efinie par z1=u1+iv1z2=u2+iv2⇐⇒ u2
1+v2 1=u2 2+v2 2.
6. Soient Eet Fdeux ensembles et f:E→Fune application. Dans Ela relation R
d´efinie par xRx0⇐⇒ f(x) = f(x0)
Exercice 6 On note Snl’ensemble des bijections (ou permutations) de σ:{1,··· , n} →
{1,··· , n}. Une permutation σest not´ee σ=1··· n
σ(1) ··· σ(n)ou simplement σ= (σ(1),··· , σ(n)).
Pour une permutation donn´ee σ, on d´efinit dans {1,··· , n}la relation ∼σpar
x∼σy⇐⇒ ∃n∈Z, σn(x) = y
1. Montrer que ∼σest une relation d´equivalence.
2. Calculer les classes d’´equivalence de ∼σpour σ=1234567
2654317
2

Exercice 7 En 1807, dans ses Recherches arithm´etiques3, Gauss ´ecrit
Nous avons adopt´e ce signe ≡`a cause de la grande analogie qui existe
entre l’´egalit´e et la congruence. C’est pour la mˆeme raison que Le Gendre
. . . a employ´e le signe mˆeme de l’´egalit´e, pour d´esigner la congruence ; nous en
avons pr´ef´er´e un autre, pour pr´evenir toute ambigu¨ıt´e.
Proposer un mod`ele de repr´esentation des classes de congruence modulo n de Zillustrant
bien le lien entre congruence et ´egalit´e pour n= 12.
3 divisibilit´e
Exercice 8 D´eterminer le quotient et le reste dans la division euclidienne de 2531 par 21.
En d´eduire le quotient et le reste dans la division de −2531 par −21, de −2531 par 21 et
de 2531 par −21.
Exercice 9 paire/impaire
1. Donner la table d’addition et de multiplication concernant la propri´et´e paire/impaire.
2. Montrer que la fonction x→x2conserve la parit´e.
3. Montrer que tout nombre rationnel peut ˆetre repr´esent´e par le quotient de nombres
entiers dont l’un au moins est impair.
4. En d´eduire que √2 n’est pas un nombre rationnel.
5. Montrer que pour tout entier naturel n,n(n+ 1) est pair.
6. Pour quels entiers nle nombre n2−1 est-il divisible par 2 ?
7. Pour quels entiers nle nombre n2−1 est-il divisible par 4 ?
8. Pour quels entiers nle nombre n2−1 est-il divisible par 8 ?
9. Pour quels entiers nle nombre n2−1 est-il divisible par 16 ?
10. Montrer que si nest le carr´e d’un entier, le reste de la division de npar 4 est 0 ou 1.
3Le texte est ´ecrit en latin requisitiones arithmetica. voici la traduction fid`ele de la d´efinition qu’il
donne: ”Si un nombre aest la mesure de la diff´erence des nombres bet c, alors bet csont dits congrus
suivant a, sinon, incongru,alui-mˆeme nous l’appelons module ; dans le premier cas, on appelle les nombres
bet cr´esidus de l’autre,non r´esidus dans le second cas ; ces notions concernent tous les nombres entiers
tant positifs que n´egatifs, mais bien ´evidemment, le module doit ˆetre pris absolument, c’est-`a-dire sans
aucun signe. Ainsi -9 et +16 sont congrus suivant le module 5; -7 est r´esidu de 15 par rapport au module
11, et non r´esidu par rapport au module 5.”
3

Exercice 10 Montrer que pour tout k entier naturel strictement positif, pour tout n
entier relatif, le nombre n(n+ 1) ···(n+k−1) est divisible par k.
Exercice 11 Peut-on trouver trois entiers cons´ecutifs dont la somme est 207 ? 328? 318?
336 ? Donner, si possible, des arguments arithm´etiques.
Exercice 12 Pour quels n∈N, 7 divise 32n−2n.
Exercice 13 L’ ´eventail myst´erieux de Lucas (R´ecr´eations math´ematiques, tome 1)
On demande `a une personne de penser un nombre entre 1 et 31. On pr´esente `a la personne
cinq panneaux correspondant aux cinq colonnes du tableau 1. On lui demande de d´esigner
les num´eros des panneaux contenant le nombre pens´e. On lui donne alors le nombre pens´e.
Expliquer l’astuce et g´en´eraliser `a n´eventails.
Table 1: Tableau de l’´eventail myst´erieux
54321
16 8 4 2 1
17 9 5 3 3
18 10 6 6 5
19 11 7 7 7
20 12 12 10 9
21 13 13 11 11
22 14 14 14 13
23 15 15 15 15
24 24 20 18 17
25 25 21 19 19
26 26 22 22 21
27 27 23 23 23
28 28 28 26 25
29 29 29 27 27
30 30 30 30 29
31 31 31 31 31
Table 2: multiplier 76 par 45
45 x 76
1 76
2 152
4 304
8 608
16 1216
32 2432
4

Exercice 14 de la multiplication ´egyptienne `a l’exponentiation rapide.
1. Montrer que tout nombre entier positif poss`ede une d´ecomposition unique en somme
de puissance diff´erentes de 2.
2. Multiplication ´egyptienne
Il s’agit de transformer une multiplication en additions `a partir d’une table de calcul
comme la table 2.
Expliquer la construction de la table, puis comment le scribe obtient 3420 en ne
faisant que des additions de nombres pr´esent dans le tableau.
3. Exponentiation rapide
Utiliser une m´ethode analogue pour calculer, pour tout entier naturel n,an`a l’aide
d’un produit de carr´es successifs de a. Exemplifier sur a11,a12 et a32.
Exercice 15 D´eterminer le pgcd et le ppcm de 35 367 et 3 258. Puis le pgcd de
35 367 000 000 et 3 258 000 000.
Exercice 16 D´eterminer les couples de Ndont le pgcd vaut 18 et la somme 360.
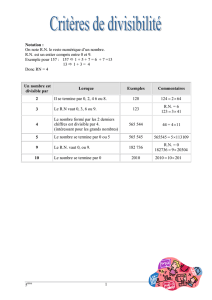
Exercice 17 Soit nun entier naturel, si n=Pk
i=0(10)iai, avec 0 ≤ai<10, on note
sa repr´esentation en base d´ecimale ak···a1a010 Prouver les crit`eres de divisibilit´e suivant
dans le syst`eme d´ecimal :
1. Un nombre est divisible par 2 ssi le dernier chiffre a0repr´esente un nombre divisible
par 2.
2. Un nombre est divisible par 3 ssi la somme de ses chiffres Pk
i=0 aiest divisible par
3.
3. Un nombre est divisible par 4 ssi a1a0repr´esente un nombre divisible par 4.
4. Un nombre est divisible par 5 ssi le dernier chiffre a0est un nombre divisible par 5.
5. Un nombre est divisible par 6 ssi la somme de ses chiffres Pk
i=0 aiest divisible par 3
et a0est pair.
6. Supposons que k= 3q+ravec q, r ∈N,r < 3 et posons am:= 0 pour tout m > k.
nest divisible par 7 si et seulement si
q
X
i=0
(−1)ia3i+2a3i+1a3i
est divisible par 7. En d´eduire que 5527579818992 est divisible par 7. Peut-on
am´eloirer le crit`ere ?
7. Un nombre est divisible par 8 ssi a2a1a0repr´esente un nombre divisible par 8.
5