s4383 - Vauban 95

1
Solution – Fonctions Numériques – Logarithmes – Etude – s4383
Soit f la fonction définie sur ] -1
2 ; +∞
∞∞
∞ [ par f(x) = -x + 7 + 6 ln (2x + 1) – 6 ln (2x + 2) .
On note (C) la courbe représentative de f dans un repère orthonormal (O ,
→
→→
→
i ,
→
→→
→
j) .
1/ Justifier que f est définie sur l’intervalle ] -1
2 ; +∞
∞∞
∞ [ .
On sait que ln A est défini si et seulement si A > 0 .
f(x) ne sera donc définie que si
2x + 1 > 0 ⇔ x > -1
2
et
2x + 2 > 0 ⇔ x > -1
ce qui impose x ∈ ] -1
2 ; +∞ [ .
2/ Déterminer la limite de f en -1
2 . En déduire que la courbe (C) admet pour asymptote une droite (D) dont on
précisera une équation.
Si x → -1
2
+
alors
-x + 7 → 13
2
2x + 1 → 0
+
⇔ ln (2x + 1) → -∞
2x + 2 → 1 ⇔ ln (2x + 2) → 0
. Par addition, on obtient : lim
x → -1
2
+
f(x) = -∞ .
La courbe (C) admet la droite x = -1
2 pour asymptote verticale.
3/ Justifier que pour tout x de l’intervalle ] -1
2 ; +∞
∞∞
∞ [ : 6 ln (2x + 1) – 6 ln (2x + 2) = 6 ln
2x + 1
2x + 2 .
On sait que pour a > 0 et b > 0 : ln a – ln b = ln a
b , d’où :
6 ln (2x + 1) – 6 ln (2x + 2) = 6 [ln (2x + 1) – ln (2x + 2)] = 6 ln
2x + 1
2x + 2
4/ Soit (D’) la droite d’équation y = -x + 7 .
a) Quelle est la limite de f(x) – (-x + 7) lorsque x tend vers +∞
∞∞
∞ ?
En donner une interprétation graphique.
f(x) = -x + 7 + 6 ln
2x + 1
2x + 2 ⇔ f(x) – (-x + 7) = 6 ln
2x + 1
2x + 2 .
Si x → +∞ alors 2x + 1
2x + 2 → 1 (rapport des plus haut degrés) et ln
2x + 1
2x + 2 → ln 1 = 0 .
On déduit : lim
x → +∞
[ f(x) – (-x + 7)] = 0 .
f(x) – (-x + 7) mesure l’écart algébrique vertical de la droite y = -x + 7 à la courbe (C) .
Cet écart devenant nul vers +∞ , on déduit que la droite (D’) d’équation y = -x + 7 est asymptote oblique à la courbe
(C) . En conséquence : lim
x → +∞
f(x) = -∞ .
b) Etudier la position de la courbe (C) par rapport à la droite (D’) .
Il faut étudier le signe de l’écart E(x) = f(x) – (-x + 7) sur l’intervalle ] -1
2 ; +∞ [ .

2
x > -1
2 ⇒ 0 < 2x + 1 < 2x + 2 ⇒ 0 < 2x + 1
2x + 2 < 1 , or 0 < A < 1 ⇒ ln A < 0 .
On déduit que E(x) = f(x) – (-x + 7) = 6 ln
2x + 1
2x + 2 < 0 sur ] -1 2 ; +∞ [ .
La courbe (C) est partout en dessous de son asymptote (D’) sur l’intervalle ] -1
2 ; +∞ [ .
5/ Montrer que pour tout x de l’intervalle ] -1
2 ; +∞
∞∞
∞ [ : f’(x) = -2x
2
– 3x + 5
(2x + 1)(x + 1) , où f’ désigne la fonction dérivée de f .
On sait que (ln u)’ = u’
u , d’où :
f(x) = -x + 7 + 6 ln (2x + 1) – 6 ln (2x + 2) ⇒ f’(x) = -1 + 6 × 2
2x + 1 – 6 × 2 2x + 2 ;
f’(x) = -1 + 12
2x + 1 – 12 2x + 2 = -(2x + 1)(2x + 2) + 12(2x + 2) – 12(2x + 1) (2x + 1)(2x + 2) = -4x
2
– 6x + 10
(2x + 1)(2x + 2) .
f’(x) = -2x
2
– 3x + 5
(2x + 1)(x + 1) .
6/ Etudier le signe de f’ et dresser le tableau de variation de f .
Recherche des Extrema :
f’(x) = 0 ⇔ -2x
2
– 3x + 5 = 0 dont les racines sont x
1
= +1 et x
2
= -5
2 .
Seule x
1
= +1 est dans le domaine de définition, avec y
1
= f(1) = -1 + 7 + 6 ln 3
4 .
y
1
= f(1) = 6 + 6 ln 3
4 ≈ 4,27 .
La courbe (C) admet F( +1 ; 6 + 6 ln 3
4 ) pour extremum.
Signe de la dérivée :
Comme 2x + 1 > 0 et 2x + 2 > 0 , la dérivée f’(x) est du signe de -2x
2
– 3x + 5 , trinôme qui est du signe de a = -2 à
l’extérieur de ses racines, et du signe opposé entre ses racines -5
2 et +1.
D’où : -1
2 < x < 1 ⇔ -2x
2
– 3x + 5 > 0 et x > 1 ⇔ -2x
2
– 3x + 5 < 0 .
Tableau de variation :
x -1/2 1 +
∞
f '(x) || + 0 –
f (x) ||-
∞
 4,27  -
∞
7/ Soit (T) la tangente à la courbe (C) au point M d’abscisse 0 de cette courbe.
Déterminer une équation de la droite (T) .
On sait que si a est l’abscisse du point de tangence, une équation réduite de la tangente (T
a
) en ce point est :
T
a
| y = f’(a)(x – a) + f(a) .
f’(0) = 5 et f(0) = 7 – 6 ln 2 .

3
D’où : T
0
| y = f’0)(x – 0) + f(0) soit T | y = 5x + (7 – 6 ln 2) .
8/ Montrer que l’équation f(x) = 2 admet une unique solution α
αα
α dans l’intervalle [1 ; 5] .
a) f est continue et strictement décroissante sur [1 ; 5] .
b) f(1) = 6 + 6 ln 3
4 ≈ 4,27 > 2 et f(5) = 2 + 6 ln 11 12 ≈ 1,48 < 2 .
Conclusion : La courbe (C) passe une et une seule fois à l’ordonnée y = 2 sur l’intervalle ]1 ; 5[ , pour une abscisse
notée α ( 1 < α < 5 ) (application du théorème de la valeur intermédiaire).
Donner une valeur de α
αα
α approchée à 10
-2
.
La calculatrice indique : α = 3,25 à 10
-2
près.
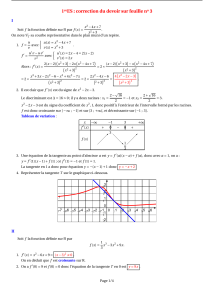
9/ Tracer les droites (D) , (D’) , (T) et la courbe (C) dans le repère (O ,
→
→→
→
i ,
→
→→
→
j) d’unité graphique 2 cm.