9. Droite – fonction affine

Cours de Seconde – 2009/2010 © EPoulin2009 Page 41
On se place dans un repère
(
)
jiO
r
r
,; orthonormé ou orthogonal.
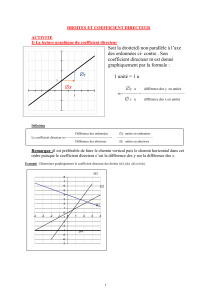
9.1. Coefficient directeur
On considère une droite
∆
, non parallèle à l’axe des ordonnées, A et B deux points distincts
de cette droite.
Le coefficient directeur de la droite est
AB
AB
xx yy
m−
−
= .
Cas particulier utilisé pour tracer une droite : si 1+=
AB
xx , alors
AB
yym −= . Ainsi,
myy
AB
+=
Si 0
>
m , la droite « monte ». Si 0
=
m la droite est « horizontale Si 0
<
m , la droite « descend ».
Deux droites sont parallèles si elles ont même coefficient directeur
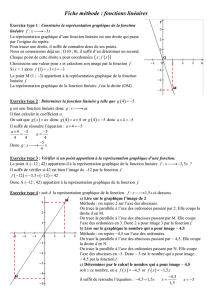
1) Comment déterminer le coefficient directeur d’une droite donnée
graphiquement ?
Méthode 1 : On repère deux points A et B de la droite, puis on calcule le coefficient directeur
avec l’égalité .
Méthode 2 : On se place sur la droite. On se décale d’une unité vers la droite et on
« descend » ou on « monte » pour rejoindre la droite. La distance ainsi parcourue donne la
valeur du coefficient directeur, positif si on est monté, négatif si on est descendu.
Exemple
2) Comment tracer une droite dont on connaît un point et le coefficient directeur ?
• On place le point connu. A partir de ce point, on se « déplace » de 1 vers la droite
parallèlement à l’axe des abscisses.
9. Droite – fonction affine
i
r
j
r
x
y
i
r
j
r
x
y
m
1
1 m
A
B
A
B
i
r
j
r
x
y A B

Cours de Seconde – 2009/2010 © EPoulin2009 Page 42
• Si le coefficient directeur est positif, on monte de sa valeur parallèlement à l’axe des
ordonnées et on marque le point.
Si le coefficient directeur est négatif, on descend de sa valeur absolue parallèlement à
l’axe des ordonnées et on marque le point.
• On trace alors la droite passant par le point de départ et ce point.
Exemple
9.2. Equation de droite
Toute droite
∆
non parallèle à l’axe des ordonnées admet une équation de la forme
p
mx
y
+
=
, où m et p sont des réels.
Le nombre m est le coefficient directeur de la droite
Le nombre p est appelé l’ordonnée à l’origine de la droite (ordonnée au point d’abscisse 0)
Dans le cas où
∆
est parallèle à l’axe des ordonnées, tous les points de la droite ont même
abscisse. Si on note k cette abscisse, la droite
∆
a pour équation kx
=
1) Comment déterminer l’équation réduite d’une droite non parallèle à l’axe des
abscisses, définie par deux de ces points ?
1. On calcule le coefficient directeur
AB
AB
xx yy
m−
−
=
2. On écrit que les coordonnées du point A vérifient l’équation réduite pmxy
AA
+= ,
puis on calcule p .
3. On écrit l’équation.
Exemple
Comment tracer une droite dont on connaît l’équation réduite y = mx + p ?
1
ère
méthode :
• On place l’ordonnée à l’origine de coordonnées
(
)
p;0
• A partir de ce point, on se déplace d’une unité vers la droite parallèlement à l’axe des
abscisses puis on monte ( si )0
>
mou on descend (si 0
<
m ) de la valeur absolue du
coefficient directeur parallèlement à l’axe des ordonnées. On marque ce point.
• On trace alors la droite passant par les deux point placés.
2
ème
méthode :
• On établit les coordonnées de deux points vérifiant l’équation de la droite. (on peut
utiliser pour cela un tableau). En prenant un troisième point, cela permet de vérifier
que les 3 points choisis sont alignés.
o Si x
A
=…, alors y
A
=
o Si x
B
=…, alors y
B
=
• On place alors ces points dans le repère, puis on trace la droite passant par ces deux
points.
Exemple

Cours de Seconde – 2009/2010 © EPoulin2009 Page 43
9.3. Exemples de problèmes
Exemple 1 :
Au stade Saint Denis, 2 tarifs sont proposés : 40€ et 55€. Lorsque le stade est plein (80000
places), Les organisateurs encaissent 3 605 000 €. Combien y a-t-il de places à 40€ ? à 55€ ?
Exemple 2 :
Dans une boulangerie, si j’achète 4 croissants et 2 pains, cela me coûte 4,34€.
si j’achète 6 croissants et 1 pains, cela me coûte 4,77€
Quel est le prix d’un pain et d’un croissant ?
1. Résolution
1.1. Méthode par substitution
on calcule une inconnue en fonction de l’autre dans une équation et on remplace cette
inconnue dans l’autre équation.
Exemples :
Ex1 : 3 8
2 5
x y
x y
+ =
− =
( )
y x
x x
= −
− − =
8 3
2 8 3 5
y x
x
= −
=
8 3
7 21 y x= − =
1
3
Vérification :
3
3
1
8
×
−
=
et
(
)
3 2 1 5− − = ,donc
(
)
{
}
S= −3 1,
Ex2 : 6 2 8
3 3
x y
x y
− =
− + =
( )
y x
x x
= +
− + =
3 3
6 2 3 3 8
y x
x
= +
=
3 3
0 14 impossible, donc
S
=
∅
1.2. Méthode par combinaisons linéaires
Après avoir multiplié chaque ligne par un nombre convenable, on ajoute les lignes
pour faire disparaître une inconnue
Ex1 :
I
II
x y
x y
2 5 21
3 4 26
+ =
− + =
3
×
I
+
2
×
II
donne
23
115
y
=
, donc
y
=
5
4
×
I
−
5
×
II
23
46
x
=
−
, donc
x
=
−
2
Vérification :
(
)
2 2 5 5 21 − + × = et
(
)
− − + × = 3 2 4 5 26, donc
(
)
{
}
S= −2 5,
Ex2 : I
II
x y
x y
6 2 8
3 4
− =
− + = −
I
II
x y
x y − × − = − = 2
6 2 8
6 2 8 On ajoute :
0
0
0
x
y
+
=
.
Les deux équations sont les mêmes
(
)
{
}
S x y IR x y= ∈ − =, /
2
6 2 8
53000 et 27000 places
0,65
€ et 0,87€

Cours de Seconde – 2009/2010 © EPoulin2009 Page 44
1.3. Méthode graphique
Exemple 1 :
I
II
x y
x y
3 8
2 5
+ =
− =
I
y
x
=
−
+
3
8
équation d’une droite D :
(
)
( )
A D
B D
0 8
2 2
,
,
∈
∈
II
( )
y x= −
1
2
5 équation d’une droite D’ :
(
)
′∈′
′−
∈′
A D
B D
5 0
05
2
,
,
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-3
-2
-1
0
1
2
3
La solution est le couple de coordonnées du point d’intersection de D et D’ :
(
)
{
}
S= −3 1, .
Exemple 2 :
6 2 8
3 4
x y
x y
− =
− + =
Les droites sont confondues

Cours de Seconde – 2009/2010 © EPoulin2009 Page 45
9.4. Fonction affine
Soit la fonction f définie par : x ax b
IR IR
a+
→
 où a et b sont des nombres réels donnés,
indépendants de x, et où a n’est pas nul : f est une fonction affine
La représentation graphique d’une fonction affine est une droite. Dans le cas d’une fonction
linéaire (b=0), la droite passe par l’origine du repère
Variations – Tableau de variations
Cas a>0
f est strictement croissante sur IR Cas a<0 f est strictement décroissante sur IR
x
−∞
+∞
x
−∞
+∞
(
)
xf
+∞
−∞
(
)
xf
+∞
−∞
Cas Particulier : La fonction identité (
x
x
a
)
C’est une droite
passant par l’origine du repère,
de coefficient directeur 1.
Exercice 37 à 44 page 72
Signe de ax+b
x
−∞
a
b
−
+∞
Signe de
ax+b
Signe de (-
a ) 0 Signe de ( a )
a>0 a<0
-5
-4
-3
-2
-1
0
1
2
3
4
5
-5 -4 -3 -2 -1 0 1 2 3 4 5