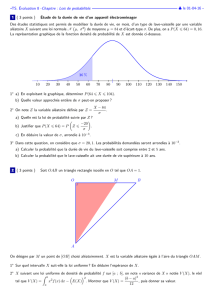
Partie 1

•A
•B
P ile
T P P ile T
P T P
P ile
P ile
P ile
P ile
P ile P ile a
G
G
a

λ Y
G
G(t) = 
1−1
tλt>1
0.
g(t)Y
A1, JA=ZA
1
λ
tλt.
Y λ
A1KA=ZA
1
λ
tλ−1t.
Y
X X = ln (Y)F
x F (x) = G(ex)
x x F (x)
X
X
λ
Z1Z2Y
T= inf (Z1, Z2)
H T x >1
P [T > x] = P ([Z1> x]∩[Z2> x])
h T
T