cours second degres

Chapitre 4 Fonctions usuelles
I) La fonction carré
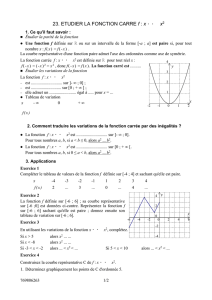
1) L`affl ˜f´o“n`cˇtˇi`o“nffl `c´a˚r˚r`é
Définition
La fonction carré est la fonction définie sur Rqui, à tout réel associe son carré.
f:x7−→ x2
Propriété
La fonction carré est croissante sur R+et décroissante sur R−.
Démonstration :
On calcule f(b)−f(a) = b2−a2= (b−a)(b+a) et on cherche le signe de f(b)−f(a).
➔1er cas I= [0; +∞[
Soit aet bde I= [0; +∞[ tels que a < b, on a donc b > a ≥0
b−a > 0
b+a > 0)(b−a)(b+a)>0
Donc pour tous 0 ≤a < b alors f(b)−f(a)>0 donc f(b)> f(a)
conclusion : La fonction carrée est strictement croissante sur [0; +∞[.
➔2ecas J=] − ∞; 0]
Soit aet bde J=] − ∞; 0] tels que a < b, on a donc a < b ≤0.
b−a > 0
b+a < 0)(b−a)(b+a)<0
Donc pour tous a < b ≤0 alors f(b)−f(a)<0 donc f(b)< f(a)
Conclusion : La fonction carrée est strictement décroissante sur ] − ∞; 0].
Tableau de variations :
x−∞ 0+∞
f:x7−→ x2
0
Le minimum de la fonction carré est 0 ; il est
atteint pour x= 0.
La courbe représentative de la fonction carré
tracée ci-contre est une parabole de sommet O
et d’axe (O;−→ j).
Courbe représentative :
1
2
3
4
5
6
7
8
9
10
-1 1 2 3-1-2-3
18

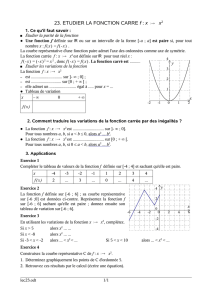
2) F`o“n`cˇtˇi`o“nffl `d`é¨fˇi‹n˚i`e `àffl ˜l„`a˚i`d`e `d`e ˜l´affl ˜f´o“n`cˇtˇi`o“nffl `c´a˚r˚r`é
Définition
Une fonction fdont l’expression algébrique peut s’écrire sous la forme f(x) = ax2+bx +coù
a6= 0 est appelée fonction polynôme de degré 2.
Soit fune fonction polynôme de degré 2.
Il est difficile en seconde d’étudier les variations avec la forme développée car la variable x
“apparait deux fois“ (dans x2et bx).
Généralement on étudie les variations sur une forme adéquate.
Voici des exemples classiques, la méthode est à connaître.
Exemple 1
Soit fla fonction définie sur Rpar f(x) = 2x2−12x+ 13.
1. Vérifier que f(x) = 2(x−3)2−5.
2. Déterminer les variations de fsur ]− ∞; 3] puis sur [3 ; +∞[.
3. Dresser le tableau de variations de fpour x∈[−1 ; 6].
4. Dresser un tableau de valeurs de la fonction fpuis tracer sa courbe représentative dans un
repère.
1. On a : 2(x−3)2−5 = 2(x2−6x+ 9) −5 = 2x2−12x+ 13 = f(x).
2. Soit aet bdeux réels de I=] − ∞; 3] tels que a < b.
opération inégalité justification
a < b ≤3
−3a−3< b −3≤0
fonction carrée (a−3)2>(b−3)2la fct. carrée est décroissante sur ]− ∞; 0]
×22(a−3)2>2(b−3)25est positif
−52(a−3)2−5>2(b−3)2−5
f(a)> f (b)
Donc la fonction fest décroissante sur ]− ∞; 3].
De même sur [3 ; +∞[, soit aet btels que 3≤a < b :
opération inégalité justification
3≤a < b
−3 0 ≤a−3< b −3
fonction carrée (a−3)2<(b−3)2la fct. carrée est croissante sur [0; −∞[
×22(a−3)2<2(b−3)25est positif
−5 2(a−3)2−5<2(b−3)2−5
f(a)< f (b)
Donc la fonction fest croissante sur [3 ; +∞[.
3. On en déduit le tableau de variations de fsur [−1 ; 6] :
x−13 6
f
27
−5
13
f(−1) = 2 ×(−1)2−12 ×(−1) + 13 = 27 et f(6) = 2 ×62−12 ×6 + 13 = 13.
Seconde Page 19

4. On dresse un tableau de valeurs :
x−10123456
f(x) 27 13 3 −3−5−3 3 13
On trace alors la courbe représentative de fdans le repère ci-dessous :
2
4
6
8
10
12
14
-2
-4
-6
1 2 3 4 5 6 7-1-2-3
Cette courbe est une parabole de sommet S(3 ; −5) et d’axe (S;−→ j).
La fonction fadmet pour minimum −5qui est atteint pour x= 3.
Propriété
Soit fun polynôme de degré 2 défini par f(x) = ax2+bx +c. Alors il existe deux réels αet
βtels que f(x) = a(x−α)2+β.
α=−b
2aet β=f(α). (à savoir par coeur)
L’expression a(x−α)2+βest appelée forme canonique du polynome f.
Preuve : a(x−α)2+β=a(x2−2αx +α2) + β=ax2−2aαx +aα2+β
Par identification avec f(x) = ax2+bx +con sait donc que
(−2aα =b
aα2+β=c⇐⇒ 
α=b
−2a=−b 2a
β=c−aα2.
Donc αet βexiste et sont uniques. De plus si on utilise f(x) = a(x−α)2+βalors on trouve
que f(α) = a(α−α)2+β= 0 + β=β
Seconde Page 20

Propriété
αest la valeur de xpour laquelle f(x)atteint son extremum qui est β:
– si a > 0, alors βest un minimum ; x−∞ α+∞
ax2+bx +c
β
– si a < 0, alors βest un maximum. x−∞ α+∞
ax2+bx +c
β
Exemple 2
Soit fla fonction définie sur Rpar f(x) = 5x2+ 8x+ 2.
1. Déterminer le tableau de variations de fsur R.
2. Dresser un tableau de valeurs de la fonction fpuis tracer sa courbe représentative dans un
repère.
1. a= 5; b= 8 et c= 2 donc α=−b
2a=−8 2×5=−0,8.β=f(α) = f(−0,8) = −1,2.
La forme canonique de fest donc f(x) = a(x−α)2+β= 5 (x+ 0,8)2−1,2.
On constate aussi que aest positif donc :
x−∞ 0,8
5x2+ 8x+ 2
−1,2
Seconde Page 21