PCMF4S – Pré calcul 40S CONTRÔLE, module 2 Trigonométrie

PCMF4S'–'Pré'calcul'40S'
CONTRÔLE,'module'2'
Trigonométrie'
!
Rédiger!les!réponses!aux!problèmes!sur!une!feuille!séparée.!Inclure!une!page%titre,!comme!pour!les!
autres!contrôles.!
!
!
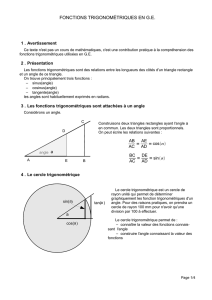
Mesure%en%radians%et%le%cercle%unitaire%%
!
1. Convertir!les!angles!suivants!en!radians.!Indiquer!la!réponse!exacte,!et!la!réponse!
approximative!arrondie!à!5!places!décimales.!
a.
€
θ =
!30°! ! ! ! c.!
€
θ =
!108°!
b.
€
θ =
!225°! ! ! ! d.!
€
θ =
!340°!
!
2. Convertir!les!angles!suivants!en!degrés.!
a.
€
θ =3
π
4
! ! ! ! c.!
€
θ =5,497787
!rads!
b.
€
θ =8
π
15
! ! ! ! d.!
€
θ =7
π
20
!
!
3. Le!point!
€
P3
8,y
"
#
$ %
&
'
!se!trouve!sur!le!cercle!unitaire!au!quatrième!quadrant.!Déterminer!la!valeur!
de!y.!
!
4. Une!mouche!se!repose!sur!le!bout!de!l’aiguille!des!secondes!d’une!horloge!pendant!40!
secondes.!Si!la!longueur!de!l’aiguille!est!de!15!cm,!quelle!distance!la!mouche!aMtMelle!voyagé!
pendant!ce!temps!?!Arrondir!la!réponse!finale!au!dixième!près.!
!
!
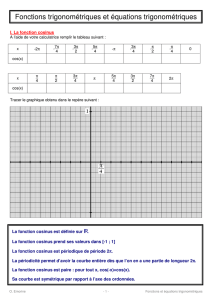
Équations%et%identités%trigonométriques%
!
5. Résoudre!les!équations!trigonométriques!suivantes!dans!l’intervalle!donné!:!
a.
€
4sin2 θ −8cos θ =−1
,!dans!l’intervalle!
€
0,2π
[ [
!
b.
€
cos2 θ +2sin θ =−sin2 θ
,!dans!l’intervalle!
€
θ ∈R
!
!
6. Exprimer!les!expressions!suivantes!sous!la!forme!d’un!seul!rapport!trigonométrique.!
a.
€
1−2sin2(37°)
!! ! ! ! b.!
€
sin2x
1−cos2 x
!!!!
!
7. Calculer!la!valeur!exacte!de!l’expression!trigonométrique!suivante!:!!
€
sin 19π
12
#
$
% &
'
(
!
!
8. Démontrer!la!preuve!de!l’identité!trigonométrique!suivante!:!! !
€
tan2 θ −1
tan2 θ +1=2sin2
θ −1
!

Fonctions%trigonométriques%
!
9. Tracer!le!graphique!de!
€
y=4 cos 2(x−π
4)
( )
+1
!dans!l’intervalle!
€
−2π,2π
[ ]
.!
!
10. Soit!la!fonction!
€
y=−1
2sin 4(x−π 6)
( )
−7
!
a. Quelle!est!l’amplitude!de!la!fonction!?!
b. Quelle!est!la!période!de!la!fonction!?!
c. Quelle!est!l’image!de!la!fonction!?!
d. Quelle!est!l’équation!de!la!ligne!horizontale!centrale!?!
e. Quelle!est!l’équation!du!même!graphique,!exprimée!en!fonction!de!cosinus!?!
!
11. Déterminer!une!équation!en!fonction!de!sinus,!et!une!équation!en!fonction!de!cosinus,!pour!
le!graphique!sinusoïdal!suivant!:!
!
!
!
12. La!hauteur!maximale!d’un!chariot!de!la!grande!roue!à!un!parc!de!divertissement!est!de!26!
mètres,!et!la!hauteur!minimale,!où!on!embarque!sur!la!roue,!est!à!une!hauteur!de!2!mètres.!
Cela!prend!8!minutes!pour!faire!le!tour!complet.!Un!édifice!avoisinant!mesure!23!m!de!haut.!
a. Déterminer!une!équation!en!forme!
€
h(t)=asin(b(t−c)) +d
!pour!la!hauteur!d’un!
chariot,!h(t),!en!mètres,!en!fonction!du!temps!écoulé,!en!minutes,!depuis!
l’embarquement!dans!le!chariot,!t.!
b. Pendant!combien!de!temps!un!passager!dans!un!chariot!pourraitMil!voir!auMdelà!de!
l’édifice!avoisinant!?!
!
!
!
CONTRÔLE,'module'2:%%%à%remettre%le%_________________________________'