objectif Noël 2016

Matière pour l’examen de Noël en mathématiques
1. Equations du second degré
C1. Connaître
1. Résoudre une équation du second degré SANS utiliser la méthode du réalisant (rhô)
lorsque c’est possible (trinôme carré parfait, méthode du produit nul, absence de terme en
x ou de terme indépendant, cfr. page 1, partie ‘Résolution’, jusque ‘j’ compris).
2. Une forme canonique d’une équation du second degré étant
,
montrer comment se trouvent les ‘formules’ des différentes solutions possibles selon
que le réalisant est strictement négatif, égal à zéro ou strictement positif.
3. Démontrer comment se trouvent les ‘formules’ de la somme (-b/a) et du produit
(c/a) des solutions (=racines) d’une équation du second degré.
4. Démontrer comment se trouve l’expression factorisée a.(x-x1).(x-x2) au départ d’un
trinôme du second degré de forme générale ax2 + bx + c dans le cas où rhô est positif.
C2. Appliquer
5. Résoudre une équation du second degré SANS utiliser la méthode du réalisant (rhô)
lorsque c’est possible (trinôme carré parfait, méthode du produit nul, absence de
terme en x ou de terme indépendant, cfr. page 1, partie ‘Résolution’, jusque ‘j’
compris).
6. Résoudre une équation du troisième degré (méthode de Horner ou tableau, puis
méthode de son choix pour le polynôme du second degré restant).
7. Résoudre une équation polynôme (cfr. page 2 exercice 4).
8. Résoudre une équation rationnelle (il y en a pas mal dans le cours).
9. Factoriser un polynôme (jusqu’au troisième degré).
10. Simplifier une fraction polynôme en donnant les conditions d’existence et de
simplification.
C3. Transférer
11. Mettre en équation et résoudre des problèmes se ramenant à une équation du second
degré (il y en a pas mal dans le cours).
POUVOIR REFAIRE LES EVALUATIONS SANS LA MOINDRE DIFFICULTE
2. Le cercle trigonométrique
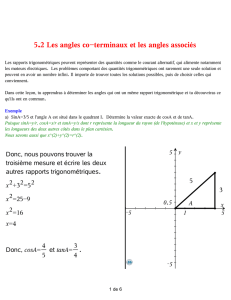
1. Connaître les formules des nombres trigonométriques dans le triangle rectangle (soh
cah toa) (C1) et pouvoir les appliquer dans les exercices (C2) et problèmes (C3).
2. Exprimer en degrés + décimales un angle exprimé en degrés + minutes + secondes (C1).
3. Connaître les différents éléments et les caractéristiques d’un cercle trigonométrique
(présentation du CT) (C1).
4. Repérer sur les axes X et Y d’un CT le sinus, le cosinus et la tangente d’un angle (C1).
5. Déterminer la valeur d’un nombre trigonométrique d’un angle dans un CT dont les
axes du repère cartésien sont gradués (C1).
6. Connaître la formule de la relation principale à la tangente (C1).
7. Connaître la formule de la relation principale au sinus et au cosinus (= relation
fondamentale). Démontrer cette formule (C1). Résoudre des exercices basés sur ces
relations principales (C2).
8. Retracer le tableau des nombres trigonométriques d’angles remarquables du premier
quadrant (C1).
9. Tracer dans un CT l’angle complémentaire ou supplémentaire d’un autre angle (C1).
10. Démontrer dans un triangle rectangle que le sinus d’un angle est égal au cosinus de
son complémentaire (C3).
11. Calculer les nombres trigonométriques (sin/cos/tan) d’angles localisés dans le second
cadran à l’aide d’angles associés et du tableau de nombres trigonométriques d’angles
remarquables du premier quadrant (C2).
12. Vérifier une égalité entre deux nombres trigonométriques d’angles différents. La
corriger si besoin et préciser de quels types d’angles associés il s’agit
(complémentaires ou supplémentaires) (C2).
13. Connaître la démonstration de la loi des sinus et celle de la loi des cosinus dans les
triangles quelconques (C1).
14. Résoudre des exercices (résolution de triangles : C2) et des problèmes (C3) basés sur
les lois des sinus et des cosinus.
POUVOIR REFAIRE LES EVALUATIONS SANS LA MOINDRE DIFFICULTE
3. Statistiques
1. A partir d’un énoncé, préciser ce que représentent la population, l’échantillon, la
variable, si cette dernière est discrète, continue, qualitative ou quantitative, donner
l’effectif de l’échantillon, les répétitions pour la énième classe (la troisième par
exemple) (C1).
2. A partir d’un tableau de données, tracer le tableau des fréquences (en %) et des
fréquences cumulées (en %) (C1).
3. A partir d’un tableau de données, tracer (C2) :
a. Le diagramme circulaire et noter les fréquences par secteur (pouvoir calculer
l’angle correspondant à chaque secteur !).
b. L’histogramme des répétitions (on dit aussi ‘des effectifs par classe’)
c. Le polygone des fréquences cumulées. Pouvoir exploiter ce graphique
comme fait au cours pour en tirer des informations.
4. A partir d’un tableau de données, calculer les valeurs centrales suivantes (C2) :
a. Le mode (+définition C1)
b. La moyenne (+formule C1)
c. La médiane