1 symétrie centrale et parallélogramme - ClicProf

1
1S SYMÉTRIE YMÉTRIE CENTRALE CENTRALE ET ET
PARALLÉLOGRAMME
PARALLÉLOGRAMME
5_4 espace et géométrie.odt clicprof.free.fr 2/13

1
1Définir la symétrie centrale et le centre de Définir la symétrie centrale et le centre de
symétrie
symétrie
Soyons curieux
Fractales : un certain motif se répète à toutes les
échelles de vision.
1.1) Définition
1. Dire que le point M' est le symétrique du point M par rapport au
point O signifie que O est le milieu du segment [MM'].
Remarque : effectuer une symétrie centrale ; c'est effectuer un demi-
tour autour d'un point.
2. Lorsque le symétrique d'une figure par rapport à un
point se superpose avec elle-même alors ce point est
un centre de symétrie de la figure.
Exemple: Le point O est le centre de symétrie de la figure.
5_4 espace et géométrie.odt clicprof.free.fr 3/13

2
2Utiliser les propriétés de la symétrie centrale Utiliser les propriétés de la symétrie centrale
Soyons curieux
2.1) Propriétés, Dans une symétrie centrale :
•L'image d'une droite est une droite qui lui est
parallèle ;
•L'image d'un segment est un segment de même
longueur ;
•L'image d'un angle est un angle de même
mesure ;
•L'image d'un cercle est un cercle de même
rayon.
2.2) Utiliser les propriétés de la symétrie centrale pour démontrer
Énoncé : Sur cette figure, M' et N' sont les symétriques de M et N par rapport à O et le
cercle (C') est le symétrique du cercle (C) par rapport à O.
Démontrer que :
1. Les droites (MN) et (M'N') sont parallèles ;
2. MN = M'N'
3.
^
MON =
^
M ' O ' N '
4. ID = I'D'
Solution :
1. Les droites (MN) et (M'N') sont symétriques par rapport à O donc (MN) // (M'N').
2. [MN] et [M'N'] sont symétriques par rapport à O donc MN =M'N'.
3.
^
MON et
^
M ' O ' N '
sont symétriques par rapport à O donc
^
MON =
^
M ' O ' N '
.
4. Les deux cercles (C) et (C') sont symétriques par rapport à O donc ID = I'D'.
2.3) Propriétés
•Lorsque deux figures sont symétriques par rapport à un point, elles sont
superposables.
•La symétrie centrale conserve les longueurs, les mesures d'angles, les périmètres et
les aires.
5_4 espace et géométrie.odt clicprof.free.fr 4/13

3
3Utiliser les propriétés des angles alternes- Utiliser les propriétés des angles alternes-
internes
internes
Soyons curieux
Molécule d'eau.
3.1) Vocabulaire
Sur la figure ci-contre, la droite (d) est sécante aux droite
(d1)et(d2). On dit que les deux angles codés sur la figure sont
alternes-internes.
3.2) Propriétés
1. Si deux angles alternes-internes sont définis par
deux droites parallèles alors ils sont égaux.
2. Si deux angles alternes-internes sont égaux alors ils
définissent deux droites parallèles.
Remarques : Le point O est le centre de symétrie de la
figure.
5_4 espace et géométrie.odt clicprof.free.fr 5/13

4
4Définir et utiliser les propriétés du Définir et utiliser les propriétés du
parallélogramme
parallélogramme
Soyons curieux
Fourche parallélogramme appelée ainsi pour la forme de la
partie bleue qui se déforme en restant un parallélogramme.
4.1) Définition
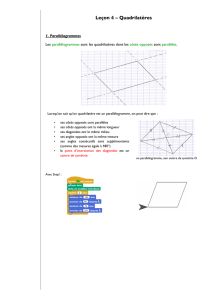
Un parallélogramme est un quadrilatère qui a ses côtés opposés parallèles.
4.2) Propriétés
1. Si un quadrilatère est un parallélogramme alors :
1. ses côtés opposés sont de même longueur ;
2. ses diagonales se coupent en leur milieu qui est
centre de symétrie ;
3. ses angles opposés sont égaux.
2. Si un quadrilatère a ses côtés opposés de même longueur alors c'est un
parallélogramme.
3. Si un quadrilatère a deux côtés opposés de même longueur et parallèles alors c'est un
parallélogramme.
4. Si un quadrilatère a ses diagonales qui se coupent en leur milieu alors c'est un
parallélogramme.
5_4 espace et géométrie.odt clicprof.free.fr 6/13