Le parallélogramme (Chap7)

Le parallélogramme (14)
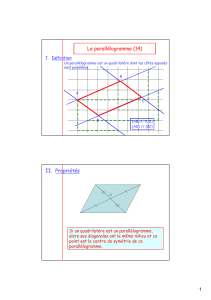
I. Définition
Un parallélogramme est un quadrilatère dont les côtés opposés
sont parallèles.
A
B
C
D(AB) // (CD)
(AD) // (BC)

II. Propriétés
Si un quadrilatère est un parallélogramme,
alors ses diagonales ont le même milieu et ce
point est le centre de symétrie de ce
parallélogramme.
O

O est le centre de symétrie, donc :
AB = CD
BC = DA
Si un quadrilatère est un parallélogramme, alors :
•ses angles opposés ont la même mesure;
•ses côtés opposés sont de même longueur.
B
C
D
A
O
ABC = CDA
BAD = DCB

Si un quadrilatère est un parallélogramme, alors :
•deux angles consécutifs sont supplémentaires
B
C
D
A
O
D1+ D2= 180°
D2= C
D2= A
Donc D1+ A = D1+ C = 180°
(angles supplémentaires)
(angles correspondants avec droites parallèles)
(angles alternes-internes avec droites parallèles)

III.Comment reconnaître un parallélogramme ?
Un quadrilatère vérifiant l’une des conditions suivantes est un
parallélogramme.
Les côtés opposés sont parallèles.
Les diagonales se coupent en leur milieu.
Alors : ABCD est un parallélogramme.
CD
O
BA
Si : O milieu de [AC] et de [BD].