série 2 - Math2Cool

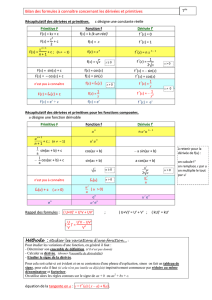
Fiche primitives : méthodes et exemples de base
Les applications du cours :
L’idée générale est de trouver la forme d’une primitive puis ensuite de rajuster en multipliant ou divisant par une
constante éventuelle.
Le terme « trouver »ne doit rien au hasard, mais à la connaissance du cours et à l’entrainement. A cet effet, j’ai rassemblé
ici les différents cas qu’il est impératif de connaître.
Voici quelques exemples/exercices rassemblés par familles : on donne le type de primitive qu’il s’agit de trouver puis
on donne plusieurs exemples à savoir faire avec la réponse en tout petit.
On notera que deux primitives d’une même fonction différant d’une constante, il suffit de déterminer une primitive pour les avoirs
toutes.
1. Une primitive de x7−→ xnest de la forme x7−→ 1
n+1xn+1pour n∈N.
Les fonctions polynômes sont continues sur Rdonc ont une primitive sur R.
(a) f(x)=2x2−7x+3.
F(x)=2
3x3−7 2x2+3x.
(b) f(x)=(x−3)5.
La formule du binôme de Newton nous permet de considérer fcomme un polynôme. Mais si il est facile
de déterminer la primitive d’un polynôme, il n’est pas très aisé d’utiliser la formule du binôme pour des
exposants élevés.
On considérera que fest sous la forme un.
Ici uest de la forme x7−→x−3 donc u0=1.
Il suffit donc de chercher Fsous la forme un+1puis de réajuster avec des constantes.
F(x)=1
6(x−3)6.
(c) f(x)=(2x+1)4.
Ici fest de la forme unavec uaffine.
uest de la forme x7−→ 2x+1 donc u0:x7−→2.
Il suffit encore de chercher Fsous la forme un+1puis de réajuster avec des constantes.
F(x)=1
5×2(2x+1)5.
(d) f(x)=x2(1 +x3)4.
Si on considère seulement (1 +x3)4on a une fonction du type u4.
On considère u5, on a : (u5)0=5×u0×u4.
En regardant bien, on s’apperçoit que fest sous la forme u0×u4donc une primitive est de la forme u5quitte
à réajuster avec des constantes.
F(x)=1
5×3(1 +x3)5.
2. Une primitive de x7−→ 1
xnest de la forme x7−→ −1 (n−1)xn−1pour n∈Net n>2.
Une fonction du type 1
uavec ucontinue admet une primitive sur tout intervalle où une s’annulle pas.
(a) f(x)=− 1
2x2+3 x3sur I=]0;+∞[.
F(x)=1
2×1 x−3 2×1
x2.
1

(b) f(x)=1
(x+4)3sur I=]−4;+∞[.
Ici on fait le même raisonnement qu’au 1.b pour 1
uet u0=1.
F(x)=−1
2×1
(x+4)2.
(c) f(x)=1
(3x+4)7sur I=]−4
3;+∞[.
Ici on fait le même raisonnement qu’au 1.c pour 1
uet u0=3.
F(x)=−1
6×3×1
(3x+4)6.
(d) f(x)=2x+5
(x2+5x)4sur I=]0;+∞[.
Ici on fait le même raisonnement qu’au 1.d pour 1
uet u(x)0=2x+5.
fest de la forme u0
u4donc une primitive sera de la forme 1 u3quitte à réajuster avec des constantes.
F(x)=−1
3×1
(x2+5x)3.
3. Une primitive de x7−→ xαest de la forme x7−→ 1
α+1xα+1pour α∈R.
Les fonctions uαadmettent une primitive sur tout intervalle où uest continue et strictement positive.
On rencontrera souvent αcaché derrière une racine carré puisque px=x1
2pour tout x>0.
(a) f(x)=− 1
2px+2pxsur I=]0;+∞[.
Soit la fonction u:x7−→px.
On a u0(x)=1
2pxsur R∗
+(c’est du cours, mais pour ceux qui ne s’en souviennent pas il est possible d’écrire
u(x)=x1
2et de calculer u0(x)=1
2x1
2−1).
D’autre part u(x)=x1
2admet une primitie U(x)=2
3x3
2.µ1
2+1=3 2¶.
F(x)=−px+2×2
3×x
3
2.
(b) f(x)=1
p3x+1sur I=]−1
3;+∞[.
fest de la forme u−1
2.
On réinvestit les connaissances du 1.c puisque uest affine avec u0=3 en notant que −1
2+1=1 2:
F(x)=2×1
3×(3x+1)
1
2.
(c) f(x)=x2−1
px+4xpxsur I=]0;+∞[.
Il faut transfomer les écritures à l’aide d’exposants :
f(x)=x2−1
x1
2+4x×x1
2=x2
x1
2−1
x1
2+4x3
2=x3 2−x−1 2+4x3 2=5x3 2−x−1 2.
F(x)=5×2
5x
5
2−2×x
1
2.
4. Une primitive de x7−→ 1
xest de la forme x7−→ln x.
(a) f(x)=x+3−7
x+2sur I=]−2;+∞[.
F(x)=1
2x2+3x−7ln(x+2).
2

(b) f(x)=x+3−7
x+2sur I=]−∞;−2[.
fest ici de la forme 1
uavec u0=1 mais avec ustrictement négatif.
Le cours nous dit qu’une primitive est alors une fonction de la forme ln|u|.
F(x)=1
2x2+3x−7ln|x+2|.
(c) f(x)=1
3x+4sur I=]−3
4;+∞[.
fest ici de la forme 1
uavec ustrictement positif et u0=3 .
Fest donc de la forme lnuquitte à réajuster avec des constantes.
F(x)=1
3×ln(3x+4).
(d) f(x)=3x2−6x+4
x3−3x2+4x−1sur Ioù le dénominateur est strictement positif.
Soit u:x7−→ x3−3x2+4x−1.
Comme uest polynomial donc continue sur Ret que lim
x→+∞u(x)= +∞ le T.V.I. généralisé nous permet d’af-
firmer qu’il existe au moins un intervalle Isur lequel u>0.
D’autre part sur un tel intervalle : u0(x)=3x2−6x+4.
Ainsi fest de la forme u0
uavec u>0.
Donc Fest de la forme lnu.
F(x)=ln(x3−3x2+4x−1).
5. Une primitive de x7−→cos xest de la forme x7−→sin xet x7−→sin xs’intégre sous la forme x7−→−cos x.
(a) f(x)=cos(3x+2).
fest de la forme cosuavec uaffine donc Fest de la forme sin uquitte à réajuster avec des constantes.
F(x)=1
3×sin(3x+2).
(b) f(x)=sin xcos4x.
Soit u:x7−→cos x. considérons naturellement u5.
On a (u5)0=5u0×u4avec u0(x)=−sin x.
Ainsi fest de la forme u0×u4donc une primitive est de la forme u5quitte à réajuster avec des constantes.
F(x)= − 1
5cos5x.
(c) f(x)=cos x
sin3xsur I=]0; π
2[.
considérons le dénominateur u:x7−→sin x.
une s’annulle pas sur I.
On considère 1
u2. On a µ1 u2¶0=−2u0 u3.
Comme u0(x)=cos x, on constate que fest de la forme u0
u3donc Fsera de la forme 1 u2quitte à réajuster avec
des constantes.
F(x)= − 1
2×1
sin2x.
6. Une primitive de x7−→ exp xest de la forme x7−→exp x.
(a) f(x)=e2x+1
fest de la forme euavec u0=2.
Donc une primitive est de la forme euquitte à réajuster avec des constantes.
F(x)=1
2e2x+1.
3

(b) f(x)=3x2ex3+5.
Soit u:x7−→ x3+5.
On considère eu. On a (eu)0=u0×eu.
Comme u0(x)=3x2, on constate que fest de la forme u0×eudonc Fsera de la forme eu.
F(x)=ex3+5.
(c) f(x)=sin x×ecos x.
Soit u:x7−→cos x.
On considère eu. On a (eu)0=u0×eu.
Comme u0(x)=−sin x, on constate que fest de la forme u0×eudonc Fsera de la forme eu.
F(x)=−ecos x.
Les méthodes :
1. Décomposer une fraction rationnelle en éléments simples.
f(x)=x2+5x−1
x+2sur I=]−2;+∞[. Il existe a,bet ctels que f(x)=ax +b+c x+2sur I.
Pour trouver fon met ax +b+c
x+2au même dénominateur puis on identifie les coefficients des polynômes
(unicité de l’écriture polynomiale).
On trouve ici a=1b=3c= −7.
Ainsi f(x)=x+3−7
x+2.
On a calculé ci-dessus (4.a) une primitive sur I:
F(x)=1
2x2+3x−7ln(x+2).
Ceux qui veulent approfondir ce type d’exercice peuvent se référer aux divers méthodes de décomposition en
éléments simples proposés dans la fiche de début d’année traitant du calcul algébrique.
2. Utiliser les formules trigonométriques.
(a) Formules usuelles.
i. f(x)=cos2x.
Il faut savoir que cos2x=cos2x−sin2x=2cos2x−1.
Donc f(x)=1
2cos2x+1 2.
F(x)=1
4sin2x+1 2x.
ii. f(x)=cos xsin x.
Il faut savoir que cos xsin x=1
2sin2x.
F(x)=1
4sin2x.
(b) Connaître la fonction tangente.
On doit savoir que d
dxtan x=1 cosx=1+tan2x. (xétant dans un intervalle sur lequel cos xne s’annulle pas).
i. f(x)=tan3x
cos2x.
On a fde la forme u0×u3car f(x)=1
cos2x×tan3xet u(x)=tan xet u0(x)=1 cos2x.
Fest donc de la forme u4quitte à multiplier par une constante.
F(x)=1
4tan4x.
ii. f(x)=1+tan2x
tan x.
fest de la forme u0
uavec u(x)=tan xcar u0(x)=1+tan2x.
Donc Fest de la forme ln|u|.
F(x)=ln|tanx|sur tout intervalle ou tan xne s’annulle pas.
4