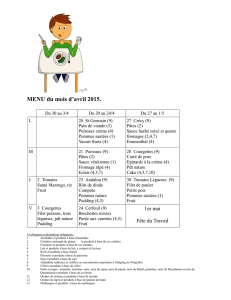
Aventures de la noix

Aventures de la noix
Jean-Yves Boislard, retraité de l’enseignement
[email protected]
À Alma, à l’occasion du dernier congrès, j’ai eu le
bonheur d’assister à l’atelier « Mission robotisée »
présenté par Frédéric Prud’homme et Brigitte Cognard. Je
les félicite pour avoir partagé avec nous cette activité. Les
élèves devaient rééchir, évaluer, calculer et se donner
des stratégies pour guider un robot devant atteindre un
colis suspect tout en contournant des obstacles. Les
élèves ressentaient tout naturellement le besoin de trouver
plusieurs moyens de vérier leur démarche et leurs
calculs, car ils n’avaient droit qu’à un essai. De plus,
l’accès au robot n’était possible qu’à la n de l’activité,
c’est-à-dire après plusieurs périodes de préparation.
Durant cet atelier, j’ai observé des réactions de participants
qui m’ont rappelé une histoire vécue que je vais vous
raconter sous une forme fantaisiste.
École des animaux instruits
Au siècle dernier, bien avant la réforme, à l’école des
animaux, le roi lion avait coné à la girafe la mission
d’enseigner les mathématiques et la physique. Un jour,
la girafe, aimant utiliser des méthodes d’enseignement
concrètes, montra cette image à ces élèves.
GRMS ENVOL no 152 — juillet-août-septembre 2010 35
La girafe dit ensuite : « Comme vous le voyez, une noix
roule sur une table puis tombe. Votre dé sera de calculer
la position à donner à la cible que doit atteindre la noix
tout en respectant les consignes suivantes :
• Vous formez des équipes de quatre animaux.
• La position de départ sur le plan incliné sera différente
pour chaque équipe et ne changera plus une fois
déterminée.
• Sur la partie plane, vous pourrez mesurer des distances et
le temps mis pour parcourir ces distances autant de fois
que vous le voudrez, pourvu que vous stoppiez la noix
au bout de la table, tout juste avant qu’elle ne tombe.
• Donc, au bout de la table, vous n’avez pas le droit de
laisser tomber la noix avant d’avoir complété tous
vos calculs. La cible vous sera d’ailleurs remise à ce
moment-là, pas avant!
• Vous n’aurez droit qu’à un seul essai; cet essai devra être
accompli en ma présence. Les autres équipes pourront
également observer votre tentative.
• Le montage de la rampe de lancement, les mesures
de distance et de temps, de même que les calculs et
l’unique essai nal devront être réalisés en une période
de 75 minutes, sans compter évidemment les périodes
précédentes de préparation théorique et stratégique.
• À cette occasion, il sera possible de vous présenter en
classe 10 minutes avant le début normal du cours. »
Stratégie de l’éléphant
L’éléphant, reconnu comme un élève brillant, pensa
réaliser l’expérience sans même utiliser les tic-tac du pic-
bois chronométreur. Il avait imaginé utiliser un bac de
sable ou une feuille de papier recouverte d’une feuille de
papier carbone; il prévoyait obtenir ainsi une trace visible
du point d’impact sur son banc.
Il espérait convaincre son équipe et surtout la girafe que
cette stratégie respectait les consignes d’une manière un
peu « élargie », mais valide.

Avec cette stratégie, il sufrait à l’équipe de mesurer la
position horizontale (en x) et la position verticale (en y) de
l’empreinte laissée par la noix. Le point de référence étant
le point de départ de la chute. Il avait d’ailleurs observé
que la trajectoire semblait être une parabole dont le point
de départ tenait lieu de sommet.
Ainsi, l’équipe présenta à la girafe la démarche suivante,
dans l’espoir de la voir approuvée :
• Le sommet étant en (0 , 0) la règle de la parabole sera
y = f(x) = ax2.
• Supposons que l’empreinte nous donne le point
(-100 , -50) avec des mesures effectuées en millimètres.
• On obtiendrait donc : -100 = a•(-50)2
• Puis : -100 = a•2500
• D’où : -0,04 = a
• Finalement : y = f(x) = -0,04 x2
Ensuite, il ne restera plus qu’à remplacer le « y » de cette
fonction par la hauteur mesurée entre la table et la cible,
pour isoler et calculer « x ». Par exemple, si la hauteur de
la table est de 900 mm, on aura :
y = -0,04 x2
-900 = -0,04 x2
22 500 = x2
± 150 = x
Dans ce cas, il sufrait de placer la cible à 150 mm à
gauche de la table et le tour sera joué!
Équipe rusée et futée!
Malheureusement, bien qu’éblouie par cette stratégie de
l’éléphant, la girafe rejeta la démarche proposée, car la
consigne de ne pas laisser la noix quitter la table avant
l’essai nal représentait une consigne incontournable.
L’éléphant, convaincu d’avoir trouvé une procédure valide,
proposa à l’équipe d’utiliser un point virtuel, imaginaire,
ou théorique : un point que la girafe ne pourrait refuser.
L’équipe se mit alors à la recherche d’informations
pouvant lui donner les coordonnées d’un mystérieux
point imaginaire. Après quelques heures de recherches, la
chauve-souris, utilisant la puissance de ses antennes et de
son radar, avait trouvé les deux informations suivantes :
• En l’absence d’air, une noix lancée horizontalement
tombe toujours de 4,90 m en une seconde, et cela, quelle
que soit sa vitesse horizontale.
• En l’absence d’air, la noix qui tombe continue d’avancer
horizontalement à la même vitesse qu’au départ.
La chauve-souris avait l’impression d’être proche de la
solution; elle avait l’intuition d’avoir trouvé le « y » de ce
point imaginaire dont la valeur serait -4900, en millimètre;
mais il manquait encore le « x » de ce point.
La chauve-souris présenta ensuite l’image ci-dessous.
Voyant cette image, le renard sauta de joie, il expliqua à
l’équipe qu’il sufra d’évaluer la vitesse de la noix sur la
table. Ainsi, disait-il, nous pourrons calculer la distance
horizontale que parcourra cette noix pendant la première
seconde de sa chute. Il ajouta, à titre d’exemple : « Si
l’on trouve que la noix roule à une vitesse de deux mètres
par seconde à la sortie de la table, on pourra en déduire
qu’elle parcourra horizontalement deux mètres pendant la
première seconde de sa chute. Cela nous donnera notre
point imaginaire (-2000 , -4900), avec des mesures en
millimètres. ».
Ainsi, on continue à utiliser la démarche proposée par
l’éléphant, sauf qu’on se servira du point imaginaire
(-2000 , -4900).
GRMS
ENVOL no 152 — juillet-août-septembre 2010
36

Résumons
1. Comme nous avons le droit de mesurer des distances
et du temps sur la table, nous évaluerons la vitesse
horizontale de la noix, tout juste avant qu’elle ne quitte
la table.
2. De cette vitesse horizontale, nous déduirons la
distance horizontale « d » que parcourra la noix en une
seconde.
3. Une information able nous dit que la noix tombera de
4900 mm pendant la première seconde.
4. Connaissant le sommet (0 , 0) de la parabole et un point
(-d , -4900), on trouvera la règle de la parabole.
5. Finalement, avec cette règle, connaissant la hauteur de
chute de la noix, nous pouvons remplacer « y » par cette
hauteur et calculer le « x » qui représente la distance
horizontale que l’on cherche.
On est prêt! La stratégie est complète.
Le doute du cheval
Le cheval aimant trotter d’un pas sûr et régulier doutait
de tout cela. Comment faire pour vérier que la noix
va réellement continuer sa vitesse horizontale pendant
sa chute? Comment savoir que ce fameux 4900 mm est
valide?
Comme nous avons droit à un seul essai, l’éléphant, le
renard et la chauve-souris se mettent d’accord pour
consulter les spécialistes en la matière, à savoir les
enseignants du département de sciences.
En collaboration avec le raton laveur, enseignant de
sciences, des photos stroboscopiques de corps en chute
libre furent prises. Ensuite, durant l’analyse de ces photos
stroboscopiques, ils tracèrent les projections horizontales
et verticales. Les analyses furent réalisées avec le chiffrier
de l’époque, un certain LOTUS.
Voici l’étude du mouvement horizontal mettant en
évidence ce mouvement très uniforme!
Par contre, lorsqu’on observe la projection verticale,
l’accélération vers le bas apparaît clairement.
Après quelques autres recherches et de la lecture sur
le sujet, notre équipe d’animaux découvrit la formule
physique qui explique ce fameux 4,9 m de chute en une
seconde; il s’agit de h = f(t) = 0,5g•t2 où :
• h : hauteur de chute (en mètres)
• t : le temps de chute (en secondes)
• g : l’accélération gravitationnelle valant généralement
entre 9,805 m/s2 et 9,820 m/s2 au Québec. Utiliser
9,81 m/s2 paraît tout à fait convenable.
GRMS ENVOL no 152 — juillet-août-septembre 2010 37

Démarche selon cette stratégie
Après ces vérications avec le raton laveur, l’équipe
envisage une nouvelle démarche possible. La voici!
1. Connaissant la hauteur de chute de la noix, la formule
physique h = f(t) = 0,5g•t2 nous permet de trouver le
temps pendant lequel la noix va tomber.
2. Nous pouvons mesurer la vitesse horizontale de la noix
sur la table.
3. Nous savons que la noix continuera horizontalement à
la même vitesse pendant la chute.
4. À partir de cette vitesse horizontale et du temps pendant
lequel la noix va tomber, nous calculerons la distance
horizontale cherchée. En effet, il suft d’utiliser la
formule très connue
vs
t
=∆
∆
reliant la vitesse uniforme
(v), la distance parcourue (Δs) et le temps écoulé (Δt).
On est prêt! Il ne reste plus qu’à préparer le montage.
Le jour magique
L’éléphant, le renard, la chauve-souris et le cheval
avaient bien hâte à ce jour. Ne prenant aucune chance,
l’équipe se présenta avant le début ofciel de la période
et prota de ces dix minutes supplémentaires offertes par
la girafe. Au moment de lancer la noix vers la cible, le
doute, l’inquiétude et l’anxiété formaient un moment de
suspense intenable. Puis, vlan! la noix enfonça le kiwi
qu’on avait placé comme cible. Toute l’équipe explosa
de joie au point où l’éléphant frappa accidentellement
la girafe au cou; elle qui s’était placée derrière lui pour
assister au lancement.
Fantaisiste, mais bien réel!
Cette histoire racontée dans un contexte fantaisiste est
fondée sur des faits réels, y compris l’accident nal. En
effet, j’ai déjà été frappé accidentellement par un élève
qui sursautait devant le succès de cette expérience. De
plus, les réactions des élèves présentées dans cet article ne
sont pas exagérées; elles sont réelles et bien perceptibles.
Comme dans les lms, seuls les noms ont été changés et
quelques éléments ctifs ont été ajoutés pour agrémenter
et soutenir l’intrigue. La noix était en réalité une bille de
métal bien lisse.
Comme enseignant de mathématiques et de physique, je
dirigeais directement mes élèves à la troisième stratégie
qui suppose une collaboration entre les départements de
mathématiques et de sciences. Cela dit, le programme de
mathématiques actuel permet très bien de réaliser les deux
premières stratégies.
Quelques conseils
o Utilisez un butoir bien ancré pour marquer le point de
départ; pas seulement une marque sur la rampe.
o Si vous lancez la bille manuellement, placez vos doigts
de chaque côté, surtout pas devant la trajectoire de la
bille. En effet, plusieurs élèves exercent une légère
poussée vers l’avant ou vers l’arrière qui n’est pas
uniforme d’un lancer à l’autre. Sans être une nécessité
absolue, l’utilisation d’un électroaimant élimine ce petit
problème.
o Dans tous les cas, mesurez avec soin et n’oubliez pas de
tenir compte de la hauteur de la cible; la bille va frapper
le haut de la cible, pas le dessous.
o Si vous chronométrez manuellement, prenez plusieurs
mesures de temps. Puisque la marge d’erreur causée
par les réexes humains est de l’ordre du dixième de
seconde, je suggère d’effectuer six mesures de temps,
dont deux pour chacune des distances horizontales
suivantes : 1,00 m, 1,25 m et 1,50 m. Vous calculerez
ensuite la vitesse moyenne des six essais. Sans être
indispensable, l’utilisation de détecteurs de mouvement
pour chronométrer électroniquement améliore la
précision.
o Sur la table, utilisez une rampe horizontale bien lisse
et bien droite. Le laboratoire de sciences en possède
probablement de bien bonnes, mais de vieilles tiges
métalliques (stores, seuil de porte, etc.) en forme de H
ou de U feraient l’affaire.
Autres informations
À la hauteur d’une table conventionnelle, les effets de la
friction de l’air commencent déjà à se faire sentir. Avec
une bille de métal de 25 mm de diamètre, une cible
d’environ 40 à 50 mm de diamètre fera très bien l’affaire
et donnera une marge d’erreur sufsante pour compenser
la résistance de l’air. N’utilisez surtout pas une balle de
ping-pong et ne placez pas la rampe de lancement à une
hauteur trop grande; dans les deux cas, l’inuence de la
résistance de l’air y sera probablement trop grande!
GRMS
ENVOL no 152 — juillet-août-septembre 2010
38

N’utilisez pas une marque ou un trait comme cible, car
les élèves percevront instinctivement le moindre écart
comme une erreur grave. J’ai déjà vu la déception dans
le visage d’élèves alors qu’ils auraient dû être ers, car
une erreur de quelques millimètres représente toute une
prouesse avec un chronométrage manuel. La cible la plus
populaire fut une petite assiette d’aluminium d’environ 4
cm de diamètre trouvée au laboratoire de sciences. En la
plaçant à l’envers, la bille l’écrase et la déforme; l’effet
est spectaculaire et l’explosion de joie assurée. J’y pense,
n’oubliez pas de permettre à vos élèves de lmer leurs
exploits!
Si ça vous intéresse, voici un site Internet donnant la
valeur de l’accélération gravitationnelle à partir de la
latitude et de l’altitude où vous réaliserez l’expérience :
http://www.ptb.de/en/org/1/11/115/_index.htm.
Au Québec, vous pouvez très bien utiliser 9,81 m/s2;
dans les faits, elle varie généralement entre 9,80 m/s2 et
9,82 m/s2.
Si vous cherchez des logiciels à utiliser pour réaliser cette
expérience, que ce soit du côté du traitement des images ou
de vidéos ou encore pour effectuer des calculs, n’hésitez
pas à consulter le site Internet de Logiciels Éducatifs
www.logicielseducatifs.qc.ca. Ce site vous présente des
logiciels disponibles au Québec. Mieux encore, il les
évalue pour vous!
Bien que les calculatrices modernes permettent de
réussir l’expérience, je suggère d’utiliser un chiffrier
électronique. Les élèves pourraient y insérer d’avance
les calculs prévus dans leur stratégie. Ainsi, pendant la
période d’expérimentation, il restera plus de temps pour
l’installation, les ajustements et les mesures.
De plus, vous trouverez une description plus
détaillée de cette expérience sur mon site Internet,
http://www.cooptel.qc.ca/~boislajy/math/. De plus, sur ce
site, vous trouverez une simulation réalisée sur Cabri et
sur GeoGebra que vous pourrez télécharger.
Aller plus loin?
Un jour, une équipe demanda de présenter l’expérience
devant des parents invités à une activité. Ils poussèrent
l’audace jusqu’à viser une autre bille qu’ils avaient placée
au sommet d’un cylindre gradué en plastique. La collision
entre les deux billes poussait la seconde dans le cylindre.
C’était tout simplement impressionnant!
Si vous souhaitez un dé encore plus difcile, vous pouvez
tenter de frapper un autre objet en mouvement.
Cela dit, si vous pensez compliquer les choses en
demandant de frapper une bille qui tombe en chute libre,
détrompez-vous. Je vous rappelle que les deux billes
tomberont à la même cadence accélérée et se frapperont
toujours! Il n’est même pas nécessaire de faire des calculs!
Il suft de s’assurer que les deux billes tombent de la même
hauteur, dans le même plan et à partir du même moment.
Dans ce cas, un détecteur de mouvement est nécessaire
pour synchroniser la chute des deux billes.
Référence
Ce récit est inspiré de « Expérience 11 : prédiction des
trajectoires » trouvée à la page 41 du guide de travail
dans le volume Les concepts du mouvement, série HPP,
tome 1. Ce volume a été publié en 1978 par l’Institut de
Recherches Psychologiques, inc.
GRMS ENVOL no 152 — juillet-août-septembre 2010 39