Chap 11 Angles dans un cercle prof

Chap 11 Angles dans un cercle
I Vocabulaire
1) Angle inscrit
Définition :
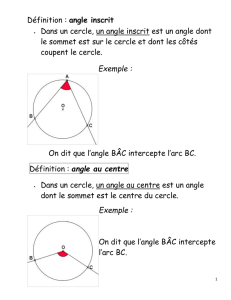
Un angle inscrit dans un cercle est un angle dont :
- le sommet est un point du cercle ;
- les côtés sont sécants au cercle en deux points distincts du cercle.
L’arc de cercle qui ne contient pas le sommet de l’angle inscrit et qui est compris entre les
deux côtés s’appelle l’arc de cercle intercepté .
Exemple 1:
Les points A, M et B sont sur le cercle (C ) de centre O.
L’angle
!
Aˆ M B
est inscrit dans le cercle (C ).
L’angle
!
Aˆ M B
intercepte l’arc de cercle AB vert.
!
Exemple 2:
Les points A’,M’,B’ sont sur le cercle (C’ ) de centre O’.
L’angle
!
A' ˆ M 'B'
est inscrit dans le cercle (C ‘).
L’angle
!
A' ˆ M 'B'
intercepte l’arc de cercle A’B’ rouge.
!
2) Angle au centre
Définition :
Dans un cercle, un angle au centre est un angle dont le sommet est le centre du cercle.
Remarque : Deux demi-droites, d’origine le centre du cercle, définissent deux angles au
centre (un angle saillant et un angle rentrant) ou (deux angles plats)
Exemple :
L’angle au centre
!
Bˆ O A
(saillant) intercepte l’arc de
cercle BA (le petit) en vert sur la figure.
L’angle au centre
!
Bˆ O A
(rentrant) intercepte l’arc de
cercle BA (le grand) en rouge sur la figure.

II Propriété de l’angle au centre :
Propriété 1 (admise) :
Si dans un cercle, un angle inscrit et un angle au centre interceptent le même arc de cercle
alors l’angle au centre mesure le double de l’angle inscrit.
Exercice résolu :
Sur la figure ci-contre, A,C,B sont des points d’un cercle
(C ) de centre O .
On sait que l’angle ACB mesure 120°.
Calculer la mesure de l’angle rentrant AOB.
L’angle au centre AOB et l’angle inscrit ACB interceptent
le même arc AB .
Donc l’angle au centre AOB mesure le double de l’angle
inscrit ACB.
!
AOB =2"Aˆ C B
AOB =2"120°
AOB =240°
Propriété 2
Si dans un cercle, deux angles inscrits interceptent le même arc de cercle alors ils ont la même
mesure.
Démonstration :
Les points B,C,D,E sont des points d’un cercle (C ) de centre A.
L’angle inscrit DEC et l’angle au centre DAC interceptent le
même arc DC.
Donc DAC=2xDEC
L’angle inscrit DBC et l’angle au centre DAC interceptent le
même arc DC.
Donc DAC=2xDBC
D’où 2xDEC=2xDBC
DEC=DBC

Cas particulier où l’angle au centre est plat :
L’angle inscrit LVM et l’angle au centre LOM interceptent le
même arc LO. Donc
!
Lˆ O M=2"Lˆ V M
Lˆ V M=1
2"Lˆ
O M
Comme LM
[ ]
est un diamètre, les points L,O,M sont
alignés et l'angle L ˆ O M mesure 180°
Lˆ V M=1
2"180°
Lˆ V M=90°
Le triangle LVM est donc rectangle en V.
Conséquence : Si un triangle est inscrit dans un cercle et que l’un de ses côtés est un diamètre
alors ce triangle est rectangle et ce côté est l’hypoténuse.
III Polygones réguliers
Définition :
Un polygone est dit régulier lorsque tous ses côtés ont la même longueur et tous ses angles
ont la même mesure.
Exemples : Le triangle équilatéral et le carré sont des polygones réguliers.
Propriété 3 (admise) :
Tout polygone régulier est inscriptible dans un cercle. Le centre de ce cercle est appelé le
centre du polygone régulier.
Exemples :

Propriété 4 (admise) :
Tous les angles au centre déterminés par deux sommets consécutifs d’un polygone régulier
(non croisé ) ont la même mesure.
Si le polygone régulier (non croisé) possède n côtés (ou n sommets) alors un angle au centre
déterminé par deux sommets consécutifs mesure
!
360°
n
.
Exemples :