Chapitre 03 Fonctions_numeriques

3Fonctions num´ eriques
Transmath 2011 p.50.
Objectifs :
– Notion de fonction ; d´eterminer un ensemble de d´efinition, une image, un ant´ec´edent
– Tracer et exploiter la repr´esentation graphique d’une fonction
–´ Etudier le sens de variation grˆace au th´eor`emes sur l’ordre, `a l’´etude de f(x0)−f(x) ; tableau de variations
et extremums
– Fonctions affine, carr´ee et inverse (vues en seconde)
– Fonctions racine carr´ee et valeur absolue
– Justifier les positions relatives des courbes repr´esentatives de x7→ x,x7→ x2, et x7→ √x
– Connaˆıtre les sens de variation des fonctions associ´ees u+k,λu,√uet 1
uo`u ket λsont des r´eels, et uune
fonction connue
– Exploiter les propri´et´es sur le sens de variation des fonctions associ´ees pour d´eterminer celui de fonctions
simples
Aper¸cu historique :
Le terme “fonction” est dˆu `a Leibniz (1692, de functio :ex´ecution), un math´ematicien allemand qui a
contribu´e `a jeter les bases de l’analyse moderne. L’id´ee de fonction a d’abord ´et´e associ´ee `a une courbe du plan
avant d’ˆetre consid´er´ee comme une combinaison d’op´eration sur une variable, ce qui peut ˆetre rapproch´e d’un
algorithme. Quelques ann´ees plus tard, Jean Bernoulli emploie la notation fx pour d´esigner une fonction de
la variable x: les fonctions telles que nous allons les ´etudier ici ´etaient n´ees.
1. Notions g´ en´ erales vues en seconde sur les fonctions num´ eriques
A. D´ efinitions et vocabulaire
D´ efinition 3.1 Une fonction num ´ erique fpermet d’associer ` a chaque nombre xd’un ensemble Dun
autre nombre que l’on note f(x). On note :
f:x7−→ f(x)
Le nombre f(x)est appel´ e image de xpar la fonction f.
L’image d’un nombre par une fonction num ´ erique est unique.
xest appel´ e ant´ ec´ edent de f(x)par f.
Un nombre peut avoir plusieurs ant´ ec´ edents ; il peut aussi ne pas en avoir.
Exemple :
On d´efinit la fonction fsur Rpar f(x) = x2−5. On a :
f:R−→ R
x7−→ x2−5
17−→ 12−5 = −4
−57−→ (−5)2−5 = 20
5
27−→ (5 2)2−5 = 25 4−5 = 5 4
π7−→ π2−5≈4,87
15

Dans cet exemple 20 a deux ant´ec´edents car l’´equation x2−5 = 20 a deux solutions : x= 5 et x=−5.
Par contre -6 n’a pas d’ant´ec´edent car x2−5 = −6 n’a pas de solution. (car x2=−1 n’en a pas.)
D´ efinition 3.2 Soit fune fonction num ´ erique. On appelle ensemble de d´ efinition de f,
et on note g´ en´ eralement Dfl’ensemble des nombres pour lesquels f(x)existe.
Exemple :
On consid`ere la fonction fd´efinie par f(x) = 3x+ 2
x−1. Le nombre f(x) existe pour tout x6= 1. En effet si
x= 1, pour calculer f(x), il faudrait diviser par 0 ce qui est impossible. Donc Df=R\ {1}.
B. Repr´ esentation graphique
D´ efinition 3.3 Soit fune fonction num ´ erique. Pour tout x∈Df, on pose y=f(x).
`
A chaque couple (x;y)on peut donc associer un point dans un rep` ere.
L’ensemble de ces points est appel´ e courbe repr ´ esentative de la fonction f. On la note g ´ en´ eralement Cf.
C. R´ esolutions graphiques d’´ equations et d’in´ equations
Soit fet gdeux fonctions num´eriques d´efinies sur un intervalle [a;b].
– R´esoudre graphiquement l’´equation f(x) = g(x) c’est trouver les abscisses des points d’intersections de Cf
et Cg.
– R´esoudre graphiquement l’in´equation f(x)≥g(x), c’est trouver les abscisses des points M(x;f(x)) et
N(x;g(x)) tels que Mest au dessus de N.
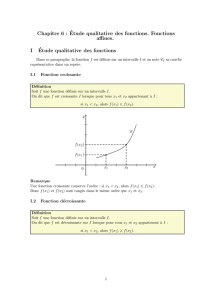
Exemple :
Sur la figure ci-dessus, on a trac´e les repr´esentations graphiques de deux fonctions fet gd´efinies sur [a;b].
L’´equation f(x) = g(x) admet trois solutions : S={x0;x1;x2}.
La solution de l’in´equation f(x)≥g(x) est S= [x0;x1]∪[x2;b].
Par exemple, pour x∈[x0;x1], on a bien M(x;f(x)) qui est au dessus de N(x;g(x)). Par contre pour
x0∈[x1;x2], on a M(x0;f(x0)) qui est en dessous de N(x0;g(x0)).
D. Variations et extremums
D´ efinition 3.4 On dit qu’une fonction fest strictement croissante sur un intervalle Isi pour tout aet bde
Itels que a<b, on a f(a)< f(b).
On dit qu’une fonction fest strictement d ´ ecroissante sur un intervalle Isi pour tout aet bde Itels que
a<b, on a f(a)> f(b).
16

Remarque :
Graphiquement, une fonction est croissante si sa courbe monte lorsqu’on se d´eplace de la gauche vers la
droite ; Et une fonction est d´ecroissante si sa courbe descend lorsqu’on se d´eplace de la gauche vers la
droite.
Fonction strictement croissante :
Pour tous les r´eels aet bde Itels que a<b, on a
f(a)< f(b).
La courbe Cfmonte lorsqu’on se d´eplace vers
la droite.
Fonction strictement d´ecroissante :
Pour tous les r´eels aet bde Itels que a < b, on a
f(a)> f(b).
La courbe Cfdescend lorsqu’on se d´eplace vers
la droite.
M´ethodes d’´etude des variations vues en seconde :
– Par lecture graphique, lorsque la fonction est d´efinie par un graphique
– Par le calcul, lorsque l’on dispose de l’expression de f(x). Pour deux valeurs x≤x0de Df, grˆace aux
th´eor`emes sur l’ordre ou en ´etudiant le signe de f(x0)−f(x), on compare f(x) et f(x0) pour appliquer la
caract´erisation ci-dessus.
D´ efinition 3.5 Soient fune fonction d ´ efinie sur un intervalle I⊂R, et a∈I.
On dit que f(a)est le minimum de fsur Isi pour tout x∈I, f(a)≤f(x).
On dit que f(a)est le maximum de fsur Isi pour tout x∈I, f(a)≥f(x).
17

2. Fonctions usuelles vues en seconde
A. Fonctions affines
Une fonction d´efinie sur Rest dite affine s’il existe deux r´eels met p
tels que pour tout x∈R, on a : f(x) = mx +p.
– Si m > 0, la fonction est croissante sur R
– Si m < 0, la fonction est d´ecroissante sur R
– Si m= 0, la fonction est constante sur R
La repr´esentation graphique d’une fonction affine dans un rep`ere est la
droite d’´equation y=mx +p.C’est une droite non parall`ele `a l’axe des
ordonn´ees, passant par le point de coordonn´ees (0; p) et de coefficient
directeur m.
B. Fonction carr´ e
La fonction carr´e est d´efinie sur Rpar x7−→ x2.
Ses variations sont les suivantes :
– elle est d´ecroissante sur ] − ∞; 0[
– elle est croissante sur ]0; +∞[
On obtient le tableau de variations :
x
f(x)
−∞ 0+∞
00
Sa repr´esentation graphique est une parabole de sommet l’origine du
rep`ere.
´
El´ements de sym´etrie : Pour tout r´eel s, on a : (−x)2=x2, donc f(−x) =
f(x). On dit que la fonction fest paire, et sa repr´esentation graphique
est alors sym´etrique par rapport `a l’axe des ordonn´ees.
18

C. Fonction inverse
La fonction inverse est d´efinie sur R∗par f(x) = 1
x.
– elle est d´ecroissante sur R∗
−
– elle est d´ecroissante sur R∗
+´egalement
Attention, elle n’est pas d´ecroissante sur R∗.
On obtient le tableau de variations :
x
f(x)
−∞ 0+∞
Sa repr´esentation graphique est une hyperbole.
´
El´ements de sym´etrie : Pour tout r´eel x6= 0 on a : ( 1
−x) =
−1
x, donc f(−x) = −f(x). On dit que la fonction fest im-
paire, et sa repr´esentation graphique est alors sym´etrique
par rapport `a l’origine.
3. Fonction racine carr´ ee
A. ´ Etude de la fonction racine carr´ ee
D´ efinition 3.6 La fonction racine carr ´ ee est la fonction d ´ efinie sur [0; +∞[qui ` a tout r´ eel positif xassocie
sa racine carr´ ee.
f:x7→ √x
Propri´ et´ e 3.1 La fonction racine carr ´ ee est croissante sur [0; +∞[.
D´ emonstration Notons f:x7−→ √x. Soient a, b ∈/R tels que 0≤a<b.
Montrons que f(a)< f(b). On va ´ etudier le signe de f(b)−f(a):
f(b)−f(a) = √b−√apour ´ etudier le signe, on essaie de factoriser
=(√b−√a)(√b+√a)
(√b+√a)cette expression existe car√b+√a > 0
=(√b)2−(√a)2
√b+√a
=b−a
√b+√a
Or a<b, donc b−a > 0. De plus, √b+√a > 0comme somme de termes strictement positifs.
Donc f(b)−f(a)>0.
Finalement, pour tous a, b ∈Rtels que 0≤a<b, on a f(a)< f (b)donc la fonction racine carr ´ ee est
croissante sur R+.
19