Activités mouvement dans un champ de forces

Mouvement dans un champ de forces
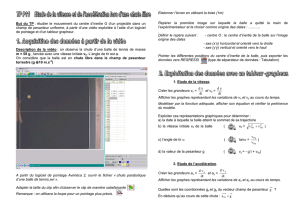
Activité : Le basketteur
On étudie la trajectoire du centre d’inertie d’un ballon de basket-ball vers le cercle du panier de
l’équipe adverse par un joueur attaquant. On ne tiendra compte ni de la résistance de l’air ni de la
rotation éventuelle du ballon. Le lancer est effectué vers le haut; on lâche le ballon lorsque son
centre d’inertie est en A (Figure ci-contre). Sa vitesse initiale est représentée par le vecteur
0
v
situé dans un plan vertical (O,
i
, j ) et faisant un angle α avec l’axe horizontal.
1- Établir les équations horaires du mouvement du centre d’inertie du ballon.
2- En déduire l’équation de la trajectoire.
3- Calculer la vitesse initiale v
0
du ballon
pour que son centre d’inertie passe
exactement au centre du cercle, le «
panier», de centre C (utiliser les valeurs
numériques fournies par la figure).
4- Un défenseur BD, placé entre l’attaquant
et le panneau de basket, saute
verticalement pour intercepter le ballon
l’extrémité de sa main se trouve en B à
l’altitude h
B
= 3,10 m. À quelle distance
horizontale maximale de l’attaquant doit-il
se trouver pour toucher le ballon du bout des doigts ?
Données : g = 9,8 m.s
-2
; α = 40° ; le diamètre du ballon est de 25 cm.
Activité : Le hockey sur gazon D’après Amérique du Nord 2009
Pratiqué depuis l'Antiquité sous le nom de « jeu de crosses », le hockey sur gazon est un sport
olympique depuis 1908. Il se pratique sur une pelouse naturelle ou synthétique, de dimensions
quasi identiques à celles d'un terrain de football. Chaque joueur propulse la balle avec une crosse ;
l'objectif étant de mettre la balle dans le but.
Dans cet exercice, on étudie le mouvement de la balle de centre d'inertie G et de masse m, dans le
référentiel terrestre supposé galiléen.
Au point B, la balle quitte la crosse à la date t = 0 avec le vecteur vitesse B v contenu dans le plan
(xOz) ; c'est la deuxième phase du mouvement.
On néglige toutes les actions liées à l'air.
On étudie le mouvement du centre d'inertie G de la balle dans le champ de pesanteur supposé
uniforme.
Le système d'axes utilisé est représenté sur le schéma ci-dessous : l'axe Ox est horizontal dirigé
vers la droite et Oz est vertical et dirigé vers le haut. L'origine des axes est située à la verticale du
point B telle que OB = h = 0,40 m.
Représentation de la flèche
et de la portée
0
vFlèche
H
Portée
x
O
k
i
z
α
S
iv=v
x0S
x
O
k
i
z
Influence de l’angle de lancer
sur la flèche et la portée
α > 45°
2
v
3
v
1
v
α = 45°
α < 45°
v
1 = v2 = v3
8
ACTIVITÉS

Données : v
B
= 14 m.s
-1
; α = 30° et g = 9,81 m.s
-1
● Partie 1 : Trajectoire de la balle.
1- Donner l'expression des coordonnées v
Bx
et v
Bz
du vecteur vitesse B v de la balle à l'instant t =
0 s, en fonction de v
B
et de α.
2- Donner l'expression des coordonnées x
B
et z
B
du vecteur
OB
de la balle au point B.
3- En appliquant la deuxième loi de Newton, déterminer les équations horaires de la balle.
4- Montrer que la valeur v
S
de la vitesse de la balle au sommet S de la trajectoire est v
S
= 12 m.s
-
1
.
5- Déterminer l’équation de la trajectoire de la balle.
● Partie 2 : But
La ligne de but est située à une distance d = 15 m du point O. La hauteur du but est L = 2,14 m.
On néglige le diamètre de la balle devant la hauteur du but.
1- Quelles conditions doivent satisfaire x et z pour que le but soit marqué ?
2- Vérifier que ces conditions sont bien réalisées.
Activité de découverte : découverte de l’électron
L'électron est une des plus importantes particules, elle est responsable en grande partie, de la
majorité des réactions chimiques et physiques de notre univers.
Sa masse est de : 9,11×10
-31
kg
Sa charge électrique est de : -1,602×10
-19
Coulomb
La découverte de l'électron s’est faite fait en plusieurs étapes : l’observation, la découverte par
Jean Perrin, sa mesure par Thomson, puis un calcul précis par Millikan.
Nous utilisons dans cette partie un tube similaire à celui utilisé par Thomson. On donne une
description dans la fiche ci-dessous.
1 Raccord pour la plaque de déviation
supérieure
2 Plaque de déviation supérieure
3 Plaque de déviation inférieure
4 Raccord pour la plaque de déviation
inférieure
5 Ecran fluorescent
6 Anode
7 Capuchon cathodique
8 Miroir à effet getter (pour le maintien du
vide)
9 Culot à broches (pour la connexion du
canon à électrons)
• L'observation
x
z
O
h
But
B α
uur
B
v

On constate un effet de fluorescence d'une ampoule de verre, contenant un gaz soumis à un
courant électrique. Cette fluorescence est due à l'impact de rayons sur le verre, qu'on nommera
rayon cathodique.
1- Peut-on faire facilement la distinction entre ce rayon cathodique et un faisceau de lumière ?
• Découverte
Jean Perrin montre qu'il ne s'agit pas en fait d'un rayonnement, mais d'un flux de particules. On se
propose de refaire cette expérience
2- Approcher un aimant du tube lorsqu’il est en fonctionnement. Que constatez-vous ? Donnez
alors les caractéristiques de la force magnétique mise alors en évidence.
On peut créer un champ magnétique uniforme grâce à un enroulement de spires dans lequel
circule un courant.
3- Que se passe-t-il lorsqu’on dévie le faisceau et qu’on le fait heurter sur une surface métallique
reliée à un électroscope.
4- De cette expérience, qu’a pu en déduire Jean Perrin ?
• Mesure
Joseph Thomson arrive à mesurer le rapport de la
charge/masse de l'électron et montre que celui-ci est
constant quel que soit le gaz utilisé. C'est donc que
l'électron est indépendant du gaz utilisé, et on en déduit
qu'il est un élément constituant l'univers et non un sous-
élément dépendant d'un autre.
Le but est de refaire l’expérience de Thomson et de
déterminer le rapport
m
e
5- En appliquant les lois de la mécanique newtonienne,
déterminer le rapport
m
e
.Comparer avec la valeur
théorique.
Activité : protons freinés
Des protons arrivent en un point O
1
avec une vitesse horizontale de valeur v
1
= 1,6×10
5
m.s
-1
et
traversent l’espace entre les deux plaques métalliques
verticales A et B percées respectivement en O
1
et O
2
.
Une tension électrique U
AB
est appliquée entre ces plaques
créant un champ électrostatique. Les protons doivent arriver au
point O
2
avec une vitesse nulle.
1- Dans quel sens est le champ
E
entre A et B ?
2- Déterminer l’expression littérale de l’accélération et la
nature du mouvement du proton entre ces deux plaques.
3- En déduire l’équation horaire du mouvement du proton.
4- Quel champ électrostatique doit-on appliquer pour le proton arrive avec une vitesse nulle en
O
2
?
A B
O
1
O
2
x
1
v
0
v
x
O
k
i
z
j
E
Déviation d’un électron par un
champ électrique