Analyse 2 CALCUL DE PRIMITIVES 1. Primitives et intégrales

Analyse 2
CALCUL DE PRIMITIVES
1. Primitives et int´egrales
D´efinition. Soient Iun intervalle de Ret une fonction f:I→R. On dit qu’une
fonction F:I→Rest une primitive de fsi
(i) Fest d´erivable ;
(ii) pour tout x∈I,F0(x) = f(x).
Th´eor`eme (admis). Toute fonction continue f:I→Radmet une primitive.
Th´eor`eme. Soit f:I→Rune fonction admettant une primitive. Alors
l’ensemble des primitives de fest {F+c, c ∈R}o`u Fest une primitive
particuli`ere.
Notation pratique. On note souvent Rf(x)dx une primitive de f(modulo une
constante additive).
D´efinition. Soit f:I→Rune fonction admettant une primitive. Etant donn´es
a, b ∈I, on d´efinit l’int´egrale de fde a`a bpar
Rb
af(x)dx =F|b
a=F(b)−F(a)
o`u Fest une primitive de f(cela ne d´epend pas de la primitive utilis´ee).
Th´eor`eme. Soient f:I→Rune fonction admettant une primitive et a∈I.
Alors G(x) = Rx
af(t)dt est la primitive de fqui est nulle en a.
Th´eor`eme (propri´et´es de l’int´egrale). Soient f, g :I→Rdes fonctions
admettant une primitive. On a :
•relation de Chasles :∀a, b, c ∈I, Rc
af(x)dx =Rb af(x)dx +Rc bf(x)dx.
•lin´earit´e : Soient λ, µ ∈R. Alors λf +µg admet une primitive sur Iet
Rb
aλf(x) + µg(x)dx =λRb af(x)dx +µRb ag(x)dx.
•positivit´e : Si a≤bet f≥0sur I, alors Rb
af(x)dx ≥0.

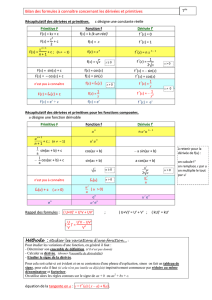
2. Utilisation d’un tableau de primitives
f(x)Zf(x)dx
xα(α6=−1) xα+1
α+ 1
1
xln |x|
exex
cos xsin x
sin x−cos x
tan x−ln |cos x|
cosh xsinh x
sinh xcosh x
tanh xln cosh x
1
x2+a2(a6= 0) 1 aarctan x a
1
√a2−x2(a > 0) arcsin x
a
f(x)Zf(x)dx
1
cos2xtan x
1
sin2x−cot x
1
cosh2xtanh x
1
1−x2
1
2ln |x+ 1 x−1|
1
√x2−1ln |x+px2−1|
1
√x2+ 1 ln(x+px2+ 1)
1
sin xln |tan x 2|
1
cos xln |tan(x 2+π 4)|
(`a savoir par coeur) (`a savoir retrouver)
3. Int´egration par parties
Th´eor`eme. Soient uet vdeux fonctions d´erivables sur l’intervalle I. Si u0vadmet
une primitive, alors uv0admet une primitive et on a
(i) Ru(x)v0(x)dx =u(x)v(x)−Rv(x)u0(x)dx ;
(ii) Rb
au(x)v0(x)dx =u(x)v(x)|b
a−Rb
av(x)u0(x)dx.
On retient cette r`egle sous la forme :
Rudv =uv−Rvdu
4. Changements de variables
Th´eor`eme. Soient ϕ:I→Rune fonction d´erivable et f:J→Rune fonction
d´efinie sur un intervalle Jcontenu dans ϕ(I).
(i) Si fadmet une primitive, alors (f◦ϕ)ϕ0admet une primitive et on a
Rf◦ϕ(x)ϕ0(x)dx =Rf(u)du.
(ii) Si ϕ0>0sur I(ou ϕ0<0sur I) et si (f◦ϕ)ϕ0admet une primitive, alors f
admet une primitive et on a Rf(u)du =Rf◦ϕ(x)ϕ0(x)dx o`u on remplace
xpar ψ(u)et ψest la fonction r´eciproque de ϕ.
2

(iii) Pour a, b ∈I, on a Rb
af◦ϕ(x)ϕ0(x)dx =Rϕ(b) ϕ(a)f(u)du.
Dans tous les cas, il faut retenir la r`egle suivante
pour le changement de variable u=ϕ(x), du =ϕ0(x)dx
et si xvarie de a`a b, alors uvarie de ϕ(a) `a ϕ(b)
5. Autres techniques
5.1. Int´egration des fractions rationnelles.
M´ethode : la d´ecomposition en ´el´ements simples (sur R) de P(x)/Q(x) r´eduit par
lin´earit´e le probl`eme `a l’int´egration des ´el´ements simples. Pas de probl`eme pour
Z1
(x−a)ndx
ou pour
Z2ax +b
(ax2+bx +c)ndx.
Pour calculer Z1
(ax2+bx +c)ndx
on compl`ete le carr´e dans ax2+bx+cpour se ramener par changement de variable
`a u2+α2. Enfin, on sait calculer
Z1
(v2+ 1)ndv.
5.2. Calcul de Z(sin x)p(cos x)qdx, o`u pet qsont entiers.
C’est facile si pou qsont impairs. Supposons par exemple q= 2k+1 impair. Alors
on fait le changement de variable u= sin x. Cela donne du = cos xdx et
Z(sin x)p(cos x)qdx =Z(sin x)p(cos x)2kcos xdx
=Zup(1 −u2)kdu
Il ne reste plus qu’`a int´egrer ce polynˆome en u.
C’est un peu plus long si pet qsont tous les deux pairs. Il faut utiliser les formules
de lin´earisation :
cos acos b=1
2(cos(a+b) + cos(a−b))
sin asin b=−1
2(cos(a+b)−cos(a−b))
sin acos b=1
2(sin(a+b) + sin(a−b))
3

5.3. Int´egration des fractions rationnelles en sin xet cos x
La m´ethode g´en´erale est le changement de variable t= tan x
2. On utilise alors les
formules suivantes :
sin x=2t
1 + t2,cos x=1−t2 1 + t2,tan x=2t 1−t2, dx =2dt 1 + t2
On est alors ramen´e `a l’int´egration d’une fraction rationnelle.
Il existe souvent des changements de variable plus ´economiques. On regarde
diverses sym´etries de l’´el´ement diff´erentiel f(x)dx sous le signe R:
Si x7→ π−xlaisse invariant f(x)dx, on pose u= sin x.
Si x7→ −xlaisse invariant f(x)dx, on pose u= cos x.
Si x7→ π+xlaisse invariant f(x)dx, on pose u= tan x.
5.4. Int´egration des fractions rationnelles en exet e−x.
Le changement de variable X=exmarche bien. En effet, on a alors dX =exdx,
d’o`u dx =dX/X. On obtient l’int´egrale d’une fraction rationnelle en X.
5.5. Elimination des radicaux.
Les changements de variable trigonom´etriques ou hyperboliques permettent
d’´ecrire certaines quantit´es comme des carr´es :
x2+ 1
´ecrivez x= tan t, alors x2+ 1 = tan2t+ 1 = 1
cos2t
ou ´ecrivez x= sinh t, alors x2+ 1 = sinh2t+ 1 = cosh2t
x2−1 avec |x|>1
´ecrivez x= cosh t, alors x2−1 = cosh2t−1 = sinh2t
1−x2avec |x|<1
´ecrivez x= sin t, alors 1 −x2= 1 −sin2t= cos2t
Un autre choix est x= cos t.
4