Polygones réguliers

Polygones réguliers
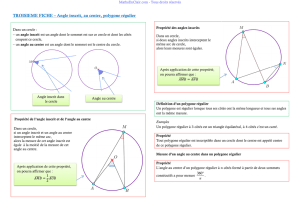
I. Généralités :
A. Définition :
Exemple : un pentagone régulier possède 5 côtés de même longueur et 5 angles égaux.
B. Propriétés :
Exemple : un carré est inscrit dans un cercle de centre O , c’est-à-dire qu’on peut tracer
un cercle qui passe par ses 4 sommets.
Exemple : un octogone régulier a ses angles au centre égaux à 
.
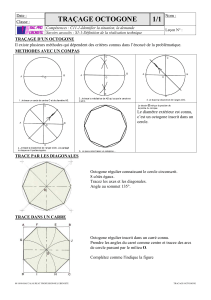
II. Construction :
A. Le triangle équilatéral :
Construire le cercle circonscrit au triangle équilatéral en traçant ses médiatrices. Leur
intersection est le centre du cercle.
B. L’hexagone régulier :
Pour construire un hexagone régulier (6 côtés), tracer un triangle équilatéral, ses médiatrices,
puis son cercle circonscrit. Les sommets de l’hexagone sont les sommets du triangle et les
points d’intersection des médiatrices avec le cercle.
C. Le carré :
Construire le cercle circonscrit au carré en traçant ses diagonales. Leur intersection est le
centre du cercle.
D. L’octogone régulier :
Pour construire un octogone régulier (8 côtés), on trace un carré, ses médiatrices, puis son
cercle circonscrit. Les sommets de l’octogone sont les sommets du carré et les points
d’intersection des médiatrices avec le cercle.
Un polygone est régulier lorsque tous ses côtés sont de même longueur et tous ses
angles sont égaux.
Propriété 1 : tout polygone régulier peut être inscrit dans un cercle.
Propriété 2 : tous les angles au centre d’un polygone régulier ont la même mesure.