Primitives calcul integral et applicationsx

N.M. Primitives. Calcul intégral. Page 1
Primitives, calcul intégral et applications
A) Calcul de primitives
1. Définition :
On appelle primitive d'une fonction f définie sur un intervalle I de toute fonction F dérivable sur I telle que pour
tout x de I : F'(x) = f(x).
2. Exemples :
Ex1.  
Ex2.  
3.
Propriétés :
 Si F est une primitive d'une fonction f sur I, alors toutes les autres primitives de f sur I sont du type x
→
F(x)+c
où c est une constante réelle.
De plus il existe une seule primitive de f sur I, qui prend la valeur y
0
en x
0
.
 Si F est une primitive de f sur l’intervalle I et G est une primitive de g sur I, alors pour tous nombres réels a et b,
aF + bG est une primitive de la fonction af +bg sur I.
 Il existe des fonctions sans primitives, cependant, toute fonction continue sur un intervalle I admet des primitives
sur I.
4.
Tableau des primitives usuelles
On désigne par F une primitive quelconque de f sur un intervalle I contenu dans l'ensemble de définition de f. x
est un élément de I.
f(x) (resp. f ) F(x) (resp. F)
0 c
a (constante) ( aU') ax+c (aU+c)
)
α
α
α U'.U ( x 1−≠
)cc
x+
+
+
+
+
+
1
1
1
α
α
α
α
1
U
(
)
x
U
U'
(
1
)ccxln ++ U(ln
)
x
2
U
U'
(
2
1
)cc
x
++−
U
1
- (
1
)
xU2
U'
(
2
1
ccx ++ U( )
)
x
eU e(U' )cc
x
e++ U (e
Cosx (U'cosU) Sinx +c ( sinU + c)
Sinx (U'sinU) - Cosx + c (- CosU + c)

N.M. Primitives. Calcul intégral. Page 2
B) Intégrale d'une fonction
5. Définition
Soit f une fonction continue sur un intervalle I de F une primitive de f sur I, a et b deux réels de I.
On appelle intégrale de a à b de la fonction f, le nombre réel F(b)-F(a). On note ce nombre
∫ ∫
b
a
,dx)x(f b
a
f(t)dt ou
On écrit : 
6. Exemples
Ex3.   . Une primitive de f sur l’intervalle [1 ; 2 ] est F(x) =
2
2
3
12
2
1
1ln))(F)(Fdx)
x
x( +=+=−=+
∫
2
1
(-ln2)(2
Ex4. Calculer 
Ex5. (D’après BTS 2010) On note    . Montrer que I = 4
7. Théorème : Intégrale et primitive
Soit f une fonction continue sur un intervalle I et a un réel quelconque de I.
La fonction F définie sur I par
∫
→x
adttfxF )(:
est l'unique primitive de f qui s'annule en a.
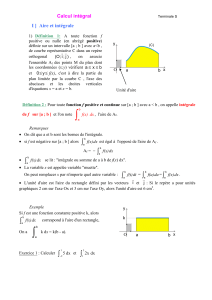
C. Application aux calculs d’aires
On donne une fonction f continue positive sur un intervalle [a , b] de
ℝ
. F est une primitive de f sur [a , b].
On désigne par (C) la courbe représentative de f dans un repère orthogonal )j,i,O( .
L'unité d'aire étant l'aire du petit rectangle
de dimensions OI et OJ ( figure ci-contre)
L'aire du domaine limité par (C) l'axe des abscisses
et les droites d'équations respectives x = a et x = b ( ba
≤
)
est égale à :
d'aire unité en
b
a
f(x)dx
∫
Si OI = 3 cm et OJ = 2 cm
Alors l'aire du domaine défini ci-dessus est :
2
cm 6
b
a
f(x)dx ×
∫

N.M. Primitives. Calcul intégral. Page 3
8. Exercice d'application :
Le plan est rapporté à un repère
orthonormal. L'unité graphique
est 1 cm .
Représenter la courbe (C)
de la fonction f définie sur [-2 , 2] par  
Calculer en cm² l'aire du domaine
limité par l'axe des abscisses la courbe (C)
et les droites d'équations respectives ;
x = -2 et x = 2.
9. Valeur moyenne :
Définition
Soit f une fonction dérivable sur un intervalle I ; soit a et b deux réels de I tel que a < b.
Le nombre réel
∫
−
b
a
dx)x(f
ab 1
s'appelle la valeur moyenne de f sur l'intervalle [a , b].
Ex6 : Calculer la valeur moyenne sur [0 ; 2] de la fonction f définie sur  par   .
10. Propriétés de l'intégrale
f et g sont des fonctions continues sur un intervalle I contenant les réels a, b et c.
β
α
et sont deux réels.
P1
∫
=
a
a
dx)x(f 0 (car F(a)-F(a) = 0)
P2
∫ ∫
−=
b
a
a
b
dx)x(fdx)x(f (car F(a) - F(b) = - ( F(b)-F(a) ) )
P3 Relation de Chasles :
∫∫ ∫
=+ c
a
dx)x(f
b
a
c
b
dx)x(fdx)x(f
P4 Linéarité de l'intégrale :
∫ ∫∫
+=+ b
a
b
a
dx)x(gdx)x(fdx)x)(
b
a
gf( βαβα .
P5 Positivité et inégalité :
[ ]
[ ]
∫∫
∫
≤≤≤
≥≥≤
b
a
dx)x(gdx)x(fa,bgfbsi
dx)x(fb,afbasi
b
a
alors sur et a
b
a
alors sur et 00
11. Inégalités de la moyenne
f est une fonction continue sur un intervalle I, contenant deux réels a et b tel que a < b.
M et m deux réels.

N.M. Primitives. Calcul intégral. Page 4
D. Intégration par parties
Soient u et v deux fonctions dérivables sur [a,b], ayant des dérivées continues sur [a,b]
La formule d'intégration par parties est :
Exemples :
Ex7. Calculer  avec x > 0.
On pose u(t) = t et v’(t) =
t
e
donc u'(t) = 1 et v(t) =
t
e
D'où
[
]
[
]
111
0
0
0
0
+−=+−=−=−= ∫∫
xxx
tx
x
xt xtx
e)x(exexedtedt)t(f ete
Ex8. (D’après BTS 2010).
1. On note    . Démontrer à l’aide d’une intégration par parties que   
2. Soit f la fonction définie par . On note   .
a. Déduire de ce qui précède (Ex5 et Ex.8.1 ) la valeur exacte de K.
b. Donner la valeur de K, arrondie à 
c. On admet que pour tout x de l’intervalle [-1 ; 1 ],   . Donner une interprétation graphique de
K.
Ex9. Calculer à l’aide d’une intégration par parties I = 0>
∫x avec
x
e
dt)t(ln .
Ex10. (D’après BTS 2007). Pour tout réel positif t, on note  
1. Montrer, à l’aide d’une intégration par parties que :   .
2. Calculer  Donner la valeur exacte de cette limite, puis sa valeur approchée arrondie à
.
Ex11. (D’après BTS 2001). Soit la fonction f définie sur  par   .
On note 
1. Montrer, à l’aide d’une intégration par parties que   .
2. Calculer la limite de  quand  tend vers -.
E. Calculs de volumes
Voir document annexe