Les différents paramètres d`une série statistique Exemple La

1
I. Les différents paramètres d’une série statistique
Exemple
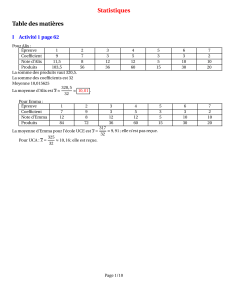
La répartition des notes des 2 classes de 1S sur une devoir commun de maths est donnée par le tableau ci-
dessous : ( toute ressemblance avec des évènements et des personnages existants ……. )
Les notations sont :
 : note ( variable statistique )
 : effectif
 : fréquence
1 1
1. Compléter les deux tableaux
2. Calculer la moyenne de chaque classe : (notées pour la et pour la )
3. Calculer pour chaque classe :
 L’étendue
 Le mode
 La médiane
 Le premier quartile
 Le troisième quartile
Parmi ces 5 paramètres caractéristiques des deux séries statistiques , lequel (ou lesquels) permet (ou
permettent ) de donner une idée de l’homogénéité ou de l’hétérogénéité des classes ?
Conclusion :
 Moyenne , médiane ,mode , quartiles sont des paramètres de position d’une série statistique
 L’étendue est un paramètre de dispersion .Elle est généralement associée au mode
Effectifs
cumulés
Fréquences
cumulées
02
2
05
2
08
3
10
5
12
4
13
3
17
3
19
2
Total
Effectifs
cumulés
Fréquences
cumulées
06
2
08
2
09
6
10
7
11
5
13
3
14
3
16
4
Total
Statistiques à une variable

2
II. Le couple (médiane – écart interquartile )
1. Rappels pour les séries à caractère discret
a. Variable discrète :
Une variable statistique est dite discrète si elle ne prend qu’un nombre fini de valeurs ( en fait : un nombre
suffisamment faible pour que l’ on puisse toutes les écrire dans un tableau )
b. Médiane :
 Lorsque les valeurs sont rangées dans l’ordre croissant , la médiane est la valeur qui laisse
autant de valeurs avant elle qu’après elle .
Il y a donc 50% des valeurs de la série qui sont plus petites que la médiane et 50% qui sont plus grandes.
 Si l’effectif total de la série est impair N = 2k + 1 , la médiane est la valeur de rang k + 1 . ( il
y en a k avant et k après )
 Si l’effectif total de la série est pair N = 2k , la médiane est la moyenne des valeurs de rang
k et k + 1
c. Quartiles :
 Le premier quartile est la première valeur de la série qui laisse 25% (donc 1/4)
des valeurs avant elle
 Le troisième quartile est la première valeur de la série qui laisse 75% ( donc 3/4)
des valeurs avant elle
d. Ecart interquartile :
 L’écart interquartile est le nombre e = , différence entre le troisième et le
premier quartile
 L’écart interquartile e est un paramètre de dispersion : 50% de l’effectif de la série est dans
l’intervalle interquartile [ ; ] , donc , plus e est petit , plus la série est concentrée autour
de la valeur médiane et plus e est important , plus la série est dispersée autour de la médiane .
e. Remarque
On peut aussi définir les neufs déciles : , , , ….. ,
et les 99 centiles : , , , ….. ,
par exemple : est la première valeur de la série qui laisse 3/10 des valeurs avant elle et est la
première des valeurs de la série qui laisse 24% des valeurs avant elle .
f. exemple :
Pour notre exemple de départ , donner les écarts interquartiles et conclure pour les comparaisons des
classes .

3
2. Cas des séries à caractère continu
a. Variable continue
Lorsqu’elle n’est pas discrète , la variable est dite continue . dans ce cas les valeurs sont regroupées dans
des intervalles : les classes de valeurs .
b. Calculs des quartiles
Les médianes , quartiles , déciles , centiles se calculent par interpolation linéaire à partir des effectifs (ou
fréquences) cumulés .
Exemple : (source INSEE )
Revenus annuels en €
(2004)
Revenus annuels en €
(2008)
Population
( en %)
Fréquences
cumulées
croissantes
[0 ; 17 000]
[0 ;18 300]
50
]17 000 ; 35 300]
]18 300 ;37000]
40
]35 300 ; 80 500]
]37 000 ;88 200]
9
]80 500 , 201 300]
]88 200 ;239 300]
0.9
]201 300 ; 551 900]
]239 300 ;732 300]
0.09
]551 900 , 3 000 000( ?)]
]732 300 ;4 000 000( ?)]
0.01
( ?) chiffre non communiqué ( pour mémoire en 2011 Michel Rollier (Michelin) a touché 4 500 000 € )
 Compléter le tableau
Remarques :
 Il est évident que , pour l’année 2004 , le revenu annuel médian est 17 000 € puisque 50% de la
population a un salaire inférieur à cette valeur .
 De même le 9 ième décile vaut 80 500 et le 99 ième centile vaut 201 300 pour 2004 .
 Le tableau étant orienté vers l’étude des hauts revenus , les autres paramètres sont entachés
d’une grosse incertitude ( on peut cependant les trouver en valeurs précises sur le site de l’INSEE)
 Calcul du premier quartile :
Il est clair que est entre 0 et 17 000 puisque 25 % est entre 0 et 50% et même dans ce cas , le calcul
est vite fait : puisque 25 % est le « milieu » de [0% ; 50%] , sera le centre de la classe [0 ; 17 000] donc
 Calcul du troisième quartile :
Il est clair que est dans ]17 000 ; 35 300] puisque 75 % est entre 50% et 90% ( 50% ont un revenu
inférieur à 17 000 € et 90% ont un revenu inférieur à 37 500 €)
Soient les points A( 17000 ; 50) et B( 35 300 ;90) du polygone des fréquences cumulées croissantes .Le
point Q( q ; 75 ) - où q est le 3ième quartile - est sur le segment [AB] en considérant que la répartition se
fait uniformément . On dit que l’on fait une interpolation linéaire
La méthode (bien connue du cours de seconde)d’identification des coefficients directeurs des droites
(confondues) (AB) et (AQ) nous permet d’écrire :
= soit = d’où q-17000 =
et donc q = 17000 +
le 3ième quartile est donc de 28 437.50 €

4
3. Représentation graphique : Diagramme en boîte (« Boîte à moustaches »)
Cette représentation fait apparaître sur un axe gradué le couple (médiane-écart interquartile)ainsi que
l’étendue .
Exemple :
Le diagramme permet de visionner immédiatement la répartition de la série et de lire :
 Médiane : 11.7 environ
 Ecart interquartile : 13-9.5 = 3.5
 Etendue : 17-7=10
25% des valeurs de la série sont entre 7 et 9.5
25% des valeurs de la série sont entre 9.5 et 11.7
25% des valeurs de la série sont entre 11.7 et 13
25% des valeurs de la série sont entre 13 et 17
 Exercice : Faire les diagrammes en boîte pour les deux classes de 1S .

5
III. Le couple (moyenne-écart type)
1. La moyenne :
Elle est notée x et donnée par x = =
On a aussi x =
Error!
= x1 f1 + x2 f2 + x3 f3 + …….+ xp fp
En effet = + + + …+ = x1 f1 + x2 f2 + x3 f3 + ...+ xpfp
 Cas d’une variable continue :
Dans ce cas les valeurs sont les centres des classes . les formules restent les mêmes .
Exercice
Un professeur de maths a donné le même contrôle dans les deux groupes de sa classe de seconde . les
notes sont les suivantes :
 Groupe 1 : 4 ; 4 ; 5 ; 8 ; 9 ;10 ; 10 ; 12 ; 12 ; 12 ; 13 ; 17 ; 18 ; 20
 Groupe 2 : 7 ; 7 ; 8 ; 9 ; 9 ; 10 ; 11 ; 11 ; 12 ; 12 ; 12 ; 14 ; 16 ; 16
a. Calculer la moyenne de chaque groupe .
b. Quel est à votre avis le groupe le plus homogène ?
c. Pour montrer la dispersion des notes par rapport à la moyenne dans chaque groupe on calcule les
écarts de chaque note par rapport à la moyenne x . Puis on calcule la moyenne de ces écarts . Que
constate-t-on ?
Groupe 1 Groupe 2
d. On calcule la moyenne des carrés des écarts (c’est la variance V) puis , pour revenir à une
grandeur correspondant à un écart , on calcule la racine carrée de cette variance ( c’est l’écart type s )
. Calculer la variance et l’écart type de chaque groupe .
e. Pour chaque groupe , quel pourcentage d’élèves ont une note comprise entre x – s et x + s ?
2. Variance et écart type
Notes
xi
Effectifs
ni
Ecart (x –
x )
Carrés des
écarts :
(x – x)2
7
8
9
10
11
12
14
16
Notes
xi
Effectifs
ni
Ecart
(x – x )
Carrés des écarts
(x – x)2
4
5
8
9
10
12
13
17
18
20