EXERCICE I. DES ÉCRITS D`ILLUSTRES SCIENTIFIQUES (6,5

BAC S Métropole 2011 EXERCICE III Spécialité : CONCERT DE VIOLONS (4 points)
Correction © http://labolycee.org
1. Le violon
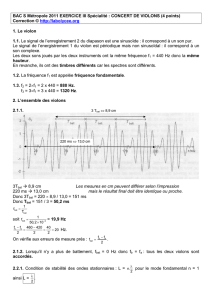
1.1. Le signal de l’enregistrement 2 du diapason est une sinusoïde : il correspond à un son pur.
Le signal de l’energistrement 1 du violon est périodique mais non sinusoïdal : il correspond à un
son complexe.
Les deux sons joués par les deux instruments ont la même fréquence f1 = 440 Hz donc la même
hauteur.
En revanche, ils ont des timbres différents car les spectres sont différents.
1.2. La fréquence f1 est appelée fréquence fondamentale.
1.3. f2 = 2f1 = 2 x 440 = 880 Hz.
f3 = 3f1 = 3 x 440 = 1320 Hz.
2. L’ensemble des violons
2.1.1.
3Tbat  8,9 cm Les mesures en cm peuvent différer selon l’impression
220 ms  13,0 cm mais le résultat final doit être identique ou proche.
Donc 3Tbat = 220  8,9 / 13,0 = 151 ms
Donc Tbat = 151 / 3 = 50,2 ms
bat bat
1
fT
soit
bat 3
1
f50,2 10
= 19,9 Hz
ba
ff 460 420 40 20
2 2 2
Hz.
On vérifie aux erreurs de mesure près :
bat
f
ba
ff
2
.
2.1.2. Lorsqu’il n’y a plus de battement, fbat = 0 Hz donc fb = fa : tous les deux violons sont
accordés.
2.2.1. Condition de stabilité des ondes stationnaires : L =
n. 2
pour le mode fondamental n = 1
ainsi L =
2
.
3 Tbat  8,9 cm
220 ms  13,0 cm

2.2.2. v = .f et  = 2.L donc pour la fréquence fondamentale f0: v = 2.L.f0
2.2.3. Analyse dimensionnelle : [F] = [m].[a] car d’après la deuxième loi de Newton une force est
homogène à une masse fois une accélération.
[F] = M.L.T2.
[µ] = [m] / [L] = M.L1
Donc :
1/2
21/2
22
1
F M.L.T L .T
M.L
= L.T1 ce qui est bien homogène à une vitesse.
La relation v =
F
est homogène.
2.2.4.
0v 1 F
f.
2.L 2.L
2.2.5. L et µ sont fixées. La fréquence est proportionnelle à la racine carrée de la tension F de la
corde. On souhaite diminuer la fréquence f0 (de 460 Hz à 440 Hz) : il faut donc diminuer la
tension F de la corde.
2.3.1. Lorsque I1 = I0 alors : L1 = 10
0
1
00
I
I
log 10 log
II
=10 log(1) = 0 dB
2.3.2. Pour un violon, on a L1 =
1
0
I
10 log I
70 dB
Pour les 10 violons : L10 = 10
11
00
10I I
log 10 log10 10 log
II
= 10 + 70 = 80 dB
2.3.3. Pour un auditeur situé à 5 m : n.I1 = I où n représente le nombre de violons.
avec I1 tel que : L1 =
1
0
I
10 log I
soit
11
0
IL
log I 10
d’où : I1 = I0 . 10L1/10
avec L1 = 70 dB il vient :
12 70/10
1
I 1,0 10 10
= 1,0×10 5 W.m2
donc n =
1
I
I
soit n =
1
5
1,0 10
1,0 10
 104 violons !
Lors d’un concert, le nombre de violons est limité à une ou deux dizaine(s) : l’intensité sonore
correspondant à des dommages de l’oreille ne sera pas atteinte.
3.1.
13 13 10 9 8 6 5 3
12 11 7 4 2
1 12 11 10 9 8 7 6 5 4 3 2 1
f f f f f f f f
f f f f f
x x x x x x x x x x 2
f f f f f f f f f f f f f
donc
12
13 i1
1i
ff2
ff
finalement :
1
i1 12
i
f2
f
.
3.2. si3 et la3 sont séparés de deux demi-tons alors :
3
3
11
si 12 12
la
f2 .2
f
avec fla3 = 440 Hz alors :
33
11
12 12
si la
f 2 .2 .f
soit
3
11
12 12
Si
f 2 2 440  
= 494 Hz.