Approche

Bac Pro date :
Ph. Georges Maths 0/7
Activité TICE : La Dérivation
Niveau : Bac Professionnel
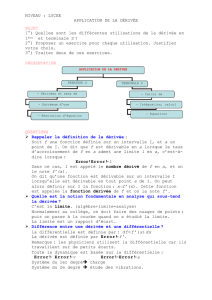
Type d'utilisation : Cours en salle d'informatique muni d'un vidéo projecteur.
Matériel : 1 ordinateur par binôme avec vidéo projecteur.
Logiciel : Graphmatica (http://www8.pair.com/ksoft/francais/about.html)
Objectifs : Vérifier la validité d'une loi, d'une hypothèse par expérimentation interactive
En prenant comme support une fonction du second degré issue d'une situation concrète (étude
cinématique du déplacement d'un véhicule), l'ordinateur permet de s'affranchir de calculs répétitifs de
nombres dérivés pour trouver la relation entre l'expression de la fonction et celle de sa fonction
dérivée.

Bac Pro date :
Ph. Georges Maths 1/7
Activité TICE : La Dérivation
I- Nombre dérivé
La Peugeot 207 1.6 HDi modèle 2006 présente les caractéristiques suivantes.
207 1.6 HDi
Prix TTC
à partir de 14 550 €
Emission CO2 (g/km)
120
Puissance (ch)
90
Cylindrée (cc)
1560
Nombre de cylindres
4
Couple maximum N.m (à tr/min)
215 (à 4000)
Vitesse maximale (km/h)
182
Accélération 0 - 100 km/h (s)
11,5
(source : http://feline207.online.fr/modules/sections/index.php?op=viewarticle&artid=11 ) :
1. Sachant que l'équation de la vitesse instantanée est v = a t (v en m/s ; accélération a en m/s 2 ; t
en s) et que la valeur de l’accélération de la Peugeot 207 est a 2,4 m/s 2, calculer les vitesses atteintes
aux temps t suivants. Arrondir les résultats à 0,1.
t (s)
0
2
5
7
10
12
15
20
v (m/s)
v (km/h)
2. En combien de temps la voiture atteindra t-elle sa vitesse maximale ? Arrondir le résultat au
dixième de seconde.
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
Rappel : l’équation horaire d’un mouvement rectiligne uniformément accéléré sans vitesse initiale a
pour expression : d =
Error!
a t 2.
3. Sachant que la valeur de l’accélération de la Peugeot 207 est a 2,4 m/s², écrire son équation
horaire lors d’un mouvement rectiligne uniformément accéléré.
…………………………………………………………………………………………………………

Ph. Georges Maths 2/7
La situation précédente peut être représentée par une fonction numérique : la branche de parabole
ci-dessous est la représentation graphique, de la fonction f définie par : f(x) = 1,2 x 2 sur [0 ; 22].
On se propose de déterminer les valeurs des coefficients directeurs des deux droites (AC) et (DB),
tangentes à la courbe respectivement aux points A et B.
3.1. A l’aide de la relation a =
Error!
, déterminer le coefficient directeur a de la droite (AC)
sachant que les coordonnées des points A et C sont les suivantes : A(10 ; 120), C(18 ; 312).
…………………………………………………………………………………………………………
3.2. Déterminer le coefficient directeur a2 de la droite (DB) sachant que les coordonnées des points D
et B sont les suivantes : D(7,5 ; 0), B(15 ; 270).
…………………………………………………………………………………………………………
3.3. Regrouper les résultats dans le tableau ci-dessous :
point
A
B
abscisse x
10
15
coefficient directeur a
A RETENIR
0
2
4
6
8
10
12
14
16
18
20
22
x
0
50
100
150
200
250
300
350
400
450
500
550
600
y
C
D
A
B
x
y

Bac Pro date :
Ph. Georges Maths 3/7
On appelle « nombre dérivé » le coefficient directeur a de la tangente au point d’abscisse xo.
Notation : f (x0) = a
4. Détermination avec le logiciel Graphmatica
1. Démarrer Graphmatica et charger le fichier derivee.gr
2. Cliquer sur le bouton « Dessiner une tangente »
3. Placer le curseur sur le point de coordonnées (0 ; 0). Ajuster la valeur de l’abscisse à 0 dans le
champ « Tracer tangente à x = » et cliquer sur calculer.
4.1. Relever la valeur du coefficient directeur et compléter le tableau de valeurs suivant en modifiant
les valeurs de x comme précédemment :
x
0
2
5
7
10
12
15
20
a
24
36
4.2. Etablir une relation entre a et x.
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
4.3. Comparer ces résultats à ceux des vitesses atteintes par l’automobile du I-1.. Conclure.
…………………………………………………………………………………………………………
…………………………………………………………………………………………………………
0
x
0
y
x
f’(x
a

Ph. Georges Maths 4/7
II- Fonction dérivée
Ouvrir un nouveau fichier dans Graphmatica. Tracer, à l’aide du logiciel, la représentation
graphiques de la fonction g telle que g(x) = – 1,5 x 2
(entrer dans le champ : y=-1.5*x^2 et appuyer sur "Entrée")
1. Tracer les tangentes pour les valeurs de x du tableau ci-dessous et relever
la valeur du nombre dérivé (coefficient directeur de la tangente).
x
– 1,5
– 1
– 0,5
0,25
1
1,5
a
2. Opérer de la même manière pour une fonction du second degré et des valeurs de x de votre choix.
Le menu déroulant du champ
"Equation" permet d’écrire l’équation
de la fonction choisie.
h : h (x) = ..........................
x
a
3. Conclure : si l’expression de la fonction est de la forme f(x) = k x 2 ; quelle est l’expression du
nombre dérivé ?
a = …………………………
A RETENIR
Définition
Soient les nombres réels a et b.
La fonction qui, à tout nombre x de l'intervalle [a ; b] associe le nombre dérivé de f en x, est appelée
fonction dérivée de la fonction f. On notre cette fonction dérivée f '.