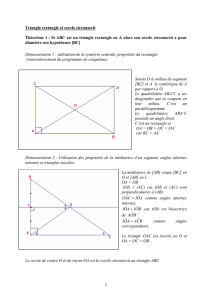
CERCLE CIRCONSCRIT TRIANGLE RECTANGLE

   !!
""#
 #"!$" " 
%&$'!"& ' ($"# " !'"
    &$" !'
)"$!  !"
#$#
#"!!   * "# 
'$ +%
#
&
#
#
&
#
'!!!!(%
#
)
#
&
#
)
#
&
#
* "# $ $! %
#
)
#
)
#
&+
#
&,-./0
#
&1./##
2,2

,$- . !$"  !$"  .($"# 
$  !$" "($    &$
($/0
1"$! !# ! 
*#
!#
0  
 !
  !"                
#!"
" &$'!"   &%#
3 
"
22 3 34
5"#       
#&$" !'"/%0
6"$! ##04!
 5# 6#  "  
 !+""+($"#   ' 
'!($7458"7#87#8
    7#8          7458  
7#87458!# 
  !    !"      7468    
!# 9!!43
 (!
!"
,#%!"#($"# $-" "!! 
   &$($
+#3"!%   !"#&$"
#3"!:3+
2+2

7$-    !$"  .#&$
$  !$" "#&$
2;2

828
#3"!!3!33<3"='!
3"!>Satz des Thales ?>Théorème de Thalès?9
!>Théorème de Thalès?::!"
!! $!3"!<3"
      3  ;   "#    @  (  
!%
4$!   ""!+$!
! ABCDEFBGHIBJKBHLDEFMBNKLKJJOJMBPBGQRIBNKCCKSF
NKL B TU B VWKNLOC B JM B"9:;<=>?@ A B@ A CD A B=<E9@ A B@F
!+# !=
$
# $-" "
+$!$"#!   
!$" "!7=8
MCFBHDSXBJKBYZHEKFLEXMBHMB[\R]U
TSBCKEFB ^_M B GT`IB MCFBNMLNMSHEX_JKELMBPBG\RI B MFB ^_M
GT`IBMCFBNKLKJJOJMBPBGQRIABHDSXBG\RIBMCFBNMLNMSHEX_JKELMBP
7#8!##
4$!   !$ aDEFB`BJMBCbYZFLE^_MBH_BNDESFBRBNKLBLKNNDLF
PBTUB`DSFLDSCB^_MBJMB^_KHLEJKFOLMB\RQ`BMCFB_SBLMXFKScJMU
$!!" 0
HMB NJ_CB`BZFKSFBJMBCbYZFLE^_MBHMBRBNKLBLKNNDLFBPBTdBJM
      !    !    #=     
"  "#- " '!
- " '  $ !!*#=
MCFB_SBNKLKJJZJDcLKYYMU
*              #      
0!#&=
 "  "#  $ !! !G!
   $ !! *
!!#=!
##
2e2