Ce cours en PDF

1UNITÉSETDIMENSIONS
Dis-moi comment l’on te cherche, je te dirai qui tu es – Bachelard
Sommaire
1.1 Grandeurs physiques et dimensions .......................... 3
1.1.1 Grandeurs physiques .............................. 3
1.1.2 Notion de dimension .............................. 3
1.1.3 Équation aux dimensions ........................... 4
1.2 Le Système International d’Unités ........................... 5
1.2.1 Les unités de base ............................... 5
1.2.2 Les unités dérivées ............................... 6
1.2.3 Préfixes SI ................................... 7
1.3 Analyse dimensionnelle ................................. 7
1.3.1 Vérifier une formule .............................. 8
1.3.2 Conversion d’unités .............................. 9
1.3.3 Modéliser .................................... 9
Ce chapitre est accessible en ligne à l’adresse :
http://femto-physique.fr/omp/grandeurs_physiques.php
2

CHAPITRE 1. UNITÉS ET DIMENSIONS 3
1.1 Grandeurs physiques et dimensions
1.1.1 Grandeurs physiques
Une grandeur physique est une quantité qui se rapporte à une propriété et qui peut se mesurer. Or,
mesurer, c’est comparer . C’est comparer à l’aide d’un instrument, une grandeur physique inconnue
avec une grandeur de même nature – on dira de même dimension – prise comme référence que l’on
appelle étalon.
Par exemple, le poids de Miss Univers peut être comparé à celui d’un étalon (1 kg par exemple) à
l’aide d’une balance : le poids de Miss Univers est une grandeur physique. En revanche, sa beauté est
une propriété subjective qui ne peut être mesurée compte tenu qu’il n’existe pas d’étalon de beauté.
En d’autres termes, la beauté se rapporte à l’aspect physique mais ne relève pas de la Physique ; il
ne s’agit pas d’une grandeur physique.
Lors du processus de mesure (mesurage) on effectue donc une comparaison entre un étalon (l’unité)
et la grandeur à mesurer puis l’on traduit le résultat par un chiffre (la mesure) assortie d’un intervalle
définissant un certain niveau de confiance (l’incertitude) ainsi que l’unité 1
X=xm±xunité
La détermination de la mesure et de l’incertitude fait l’objet d’un autre chapitre. Ici on s’intéresse
au contenu dimensionnel des grandeurs physiques et du choix de l’unité.
1.1.2 Notion de dimension
En général, le résultat d’une mesure dépend de l’étalon utilisé. Par exemple, si l’on compare la
longueur ¸ d’une règle de 1 m avec un décimètre, on obtient ¸ = 10 dm. Si l’on choisit un double
décimètre comme étalon de mesure, on trouve ¸ =5ddm (double décimètre). La mesure est donc
différente (5,10) : on dit que la longueur possède une dimension.
Par définition, une grandeur physique G a une dimension si sa mesure dépend du choix de l’étalon
de mesure. Sa dimension est notée [G].
Il ne faut pas confondre cette notion avec l’unité qui est purement conventionnelle alors que la
dimension est une propriété indépendante de tout système d’unités.
Deux grandeurs ont même dimension si on peut les comparer. C’est pourquoi le rayon d’un cercle et
son périmètre ont même dimension, car je peux en faire la mesure avec le même étalon (par exemple
un fil souple d’une certaine longueur). Ici il s’agit de la dimension [longueur].
Il existe également des grandeurs physiques sans dimension (on dit aussi adimensionnées). Dans
ce cas la dimension est noté [ G ]=1. Par exemple, l’angle ◊ d’un secteur AOB est une grandeur
que l’on peut mesurer comme suit : traçons un cercle de centre O et de rayon r . Les droites (OA)
1 . L’unité est indispensable ! Exprimer le résultat d’un calcul ou d’une mesure sans préciser l’unité n’a aucun sens.

CHAPITRE 1. UNITÉS ET DIMENSIONS 4
et (OB) coupent le cercle en deux points A’ et B’. L’angle se mesure en faisant le rapport de la
longueur d’arc
)
AÕBÕet du rayon du cercle.
•B
•
O•A
A’
B’
r
◊
ש
)
AÕBÕ
r
On constate donc que si l’on double le rayon du cercle, la longueur d’arc double également de sorte
que l’angle ne dépend pas de la taille du cercle. Il est alors assez évident que si l’on décide de mesurer
les distances en centimètre, en pouce, ou dans n’importe quel système d’unités, le résultat de l’angle
◊ ne changera pas. L’angle est donc sans dimension . De la même manière, une grandeur définie
comme le rapport de deux grandeurs de même dimension, ne présente pas de dimension.
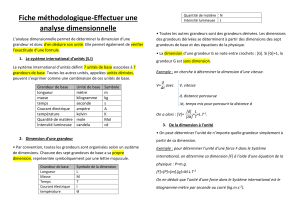
Enfin, par commodité, on a donné un nom spécifique à certaines dimensions
Dimension Symbole
Longueur L
Masse M
Temps T
Intensité électrique I
Température ⇥
Quantité de matière N
1.1.3 Équation aux dimensions
Une loi physique affirme l’égalité de deux grandeurs qui sont nécessairement de même nature. Une
loi physique est donc aussi une relation entre différentes dimensions : on parle d’ équation aux
dimensions. Voyons comment obtenir ces équations aux dimensions sur quelques exemples.
La vitesse : d’après la définition vx©dx/dt, on déduit
[v]=LT≠1
L’accélération : la définition ax©dvx/dtdonne
[a]=[v]
T=LT≠2
La force : en vertu de la deuxième loi de Newton F=ma on a
[F]=MLT≠2

CHAPITRE 1. UNITÉS ET DIMENSIONS 5
La constante des gaz parfaits : on peut obtenir sa dimension à partir de la loi du gaz parfait
pV =nRT .
[R]=[p][V]
[n][T]=[F] L2◊L3 N⇥=ML2T≠2⇥≠1N≠1
Le champ magnétique : par définition du champ magnétique, une particule de charge électrique q
se déplaçant à la vitesse
≠æv
dans un champ magnétique
≠æB
subit une force
≠æF
= q≠æv·≠æB , d’où
[B]= [F]
[q][v]=MLT≠2
IT ◊LT≠1=MT≠2I≠1
1.2 Le Système International d’Unités
Comme on l’a déjà dit, mesurer c’est comparer une grandeur physique avec un étalon qui définit
l’ unité de mesure . Celle-ci relevant d’un choix arbitraire il faut bien convenir d’un système d’unités
pour pouvoir communiquer (transactions commerciales, rapports scientifiques, etc.). La bonne idée
consiste alors à choisir des étalons dont la définition est indépendante du lieu et du temps et avec
lesquels on peut construire toutes les unités. C’est l’ambition du système d’unités internationales
(SI) adopté par quasiment tous les pays
2
. Né officiellement en 1960, il s’agit d’une extension de
l’ancien système MKSA.
1.2.1 Les unités de base
Le (SI) forme un système cohérent reposant sur sept unités de base (cf. tableau 1.1) indépendants
du point de vue dimensionnel.
Dimension Symbole Unité SI Symbole
Longueur L mètre m
Masse M kilogramme kg
Temps T seconde s
Intensité électrique I ampère A
Température ⇥kelvin K
Quantité de matière N mole mol
Intensité lumineuse J candela cd
Table 1.1 – Les sept unités de base du Système Internationale d’Unités.
En attendant une éventuelle révision de ces unités prévue en 2018, nous en donnons ici les définitions
actuelles.
Le mètre est relié à la seconde via l’invariance de la vitesse de la lumière dans le vide. Par définition,
la distance parcourue par la lumière dans le vide pendant une seconde vaut L = 299792458 m
2 . Trois pays n’ont pas encore adopté officiellement le système métrique : le Libéria, la Birmanie et. . . les Etats-Unis.

CHAPITRE 1. UNITÉS ET DIMENSIONS 6
Remarque : le mètre a connu en deux siècles quatre définitions successives. Initialement, le mètre
était défini à partir de la longueur du méridien terrestre supposé invariable : L =40000 km .
Aujourd’hui, avec l’étalon mètre actuel (lié à l’étalon seconde) L =40008 , 08 km ; la différence est
donc imperceptible pour un utilisateur courant.
Le kilogramme est la masse d’un bloc cylindrique de Platine irridié (90%Pt-10%Ir) conservé au
pavillon de Breteuil (Sèvres) depuis 1889.
Remarque : cet étalon se dégrade par usure et contamination ; c’est pourquoi il est envisagé de
changer de définition du kg et de définir cette unité à partir de la constante de Planck h.
La seconde est la durée de 9192631770 périodes de la radiation correspondante à la transition entre
les deux niveaux hyperfins de l’état fondamental de l’atome
133Cs
au repos dans le référentiel
d’étude.
Remarque : initialement la seconde était définie à partir du jour solaire moyen J par la relation
J=86400s. Aujourd’hui, avec la définition de l’étalon seconde, on a J=86400,003s.
L’ampère est défini à partir de la force magnétique de Laplace et permet d’établir à 10
≠7
près
les principaux étalons du domaine électrique. Un ampère est l’intensité du courant qui fait
apparaître une force de 2 . 10
≠7N
entre deux conducteurs filiformes rectilignes infinis distants
de 1m, parcourus par ce courant électrique.
Remarque : cette définition fixe les valeurs de la perméabilité magnétique et de la permittivité du
vide à
µ0=4fi.10≠7H.m≠1et ‘0=1
µ0c2
Notez qu’il est prévu de redéfinir l’ampère à partir de la charge de l’électron e ce qui aura pour
effet de fixer la valeur de e mais de rendre à µ0 et à ‘0 leur statut de constantes expérimentales.
Le kelvin se rapporte à la loi du gaz parfait. Par définition du kelvin, la température d’un gaz
parfait en équilibre avec l’eau dans ses trois états (le point triple de l’eau) vaut 273,16 K.
Remarque : la future définition du kelvin fixera la valeur de la constante de Boltzmann kB.
La mole est la quantité d’atomes contenue dans 12 g de carbone 12.
Remarque : l’imprécision de cet étalon est donc liée à celle de la masse. Pour pallier cet inconvénient,
il est envisagé de définir la mole en fixant la valeur du nombre d’Avogadro.
La candela est l’unité donnant l’intensité lumineuse d’une source dans une direction donnée. Par
définition, 1 cd est intensité lumineuse d’une lumière verte de fréquence ‹ = 540 . 10
12 Hz
rayonnant 1
683 W.sr≠1.
1.2.2 Les unités dérivées
Les sept unités de base du système international sont les « unités fondamentales » à partir desquelles
sont obtenues par combinaison toutes les autres unités, dites unités dérivées . Certaines d’entre-elles