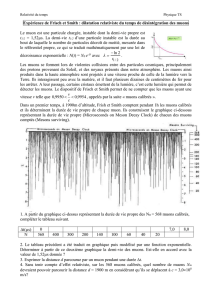
20 10 6,7 10 s 67 10 s 0,9994 299792458 t × ∆ = = × = × × d

Bac S Polynésie septembre 2015 CORRECTION © http://labolycee.org
EXERCICE I : Le muon, explorateur de volcan (6 points)
1. Les muons créés en haute atmosphère
1.1. Dilatation des durées
1.1.1. D’après le 1
er
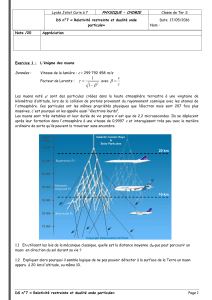
document : « Un muon créé à une hauteur de 20 km doit mettre environ 67 µs
pour arriver au sol ».
Or il est indiqué que les muons se déplacent quasiment à la vitesse de la lumière dans le vide, on
peut par exemple prendre la valeur indiquée pour les muons du CERN v = 0,9994.c.
Comme
d
v
t
=
∆
alors
0,9994.
d d
t
v c
∆ = =
3
5 6
20 10
6,7 10 s 67 10 s
0,9994 299792458
t
− −
×
∆ = = × = ×
×
= 67 µs On retrouve la valeur indiquée.
Remarque : on pouvait se contenter de faire le calcul avec la valeur approchée de
c = 3,0×10
8
m.s
-1
.
1.1.2. En 1905, Einstein postule que : « La valeur de la vitesse de la lumière dans le vide est la
même dans tous les référentiels galiléens ».
1.1.3. Définissons les deux évènements entre lesquels sont mesurées les durées évoquées ici.
Évènement 1 : Création du muon dans la haute atmosphère.
Évènement 2 : Détection du muon au niveau du sol.
Dans le référentiel propre, ces deux évènements ont lieu au même endroit. Il s’agit, ici, du
référentiel « muon ». Dans le référentiel propre, on mesure la durée propre ΔT
0
.
Dans le référentiel terrestre, on mesure la durée mesurée ΔT (ou durée impropre).
La durée mesurée ΔT de 67 µs a subi le phénomène de « dilatation des durées » : ΔT = γ.ΔT
0
(avec γ ≥ 1). Pour le muon, il s’est écoulé une durée ΔT
0
bien plus courte et donc inférieure à sa
durée de vie ; ce qui explique que le muon ne soit pas encore désintégré et qu’il soit détecté au
niveau du sol.
1.2. D’après les données : la force magnétique a une intensité proportionnelle à la vitesse de la
particule, à la valeur absolue de sa charge et au champ magnétique mais cette force est
indépendante de la masse de la particule.
Ici, les 3 particules (proton, muon, électron) ont la même vitesse et la même valeur absolue de
charge (= e) : la force magnétique qu’ils subissent, dans le même champ magnétique, est donc de
même intensité.
Différence de courbure :
La masse n’intervient pas dans l’intensité de la force, mais elle intervient sur les effets de cette
force.
D’après la deuxième loi de Newton, appliquée à la particule de masse m constante, dans le
référentiel terrestre :
ext
F
dv
a
dt m
Σ
= =
.
Pour une même force subie, plus la masse de la particule est grande et plus son accélération
a
sera faible. Le vecteur vitesse
v
varie moins en direction, la trajectoire est moins courbée.
Comme la trajectoire d’un muon est moins incurvée que celle d’un électron mais plus incurvée que
celle d’un proton, on peut en déduire que le muon a une masse intermédiaire entre celle du proton
et celle de l’électron.
Remarque : On souhaite faire tourner brusquement un caddie de supermarché. Si on applique
une même force à ce caddie, il est d’autant plus facile de le faire tourner que sa masse est faible.

2. Les muons au CERN
2.1. Justifier l’affirmation « Ces muons ont un temps de vie environ égal à 30 fois leur temps de
vie au repos » revient à démontrer que le facteur de Lorentz γ est environ égal à 30.
En effet ΔT temps de vie mesuré dans le référentiel terrestre du laboratoire et ΔT
0
temps de vie au
repos (dans le référentiel du muon) sont liés par ΔT = γ.ΔT
0
.
1
²
1
²
v
c
=−
γ
ici v = 0,9994.c donc
v
c
= 0,9994
2
1
1 0,9994
γ
=−
= 28,87
Ce résultat est proche de la valeur annoncée d’environ 30.
2.2. Comme le facteur de Lorentz est égal à 28,87, la durée de vie des muons ΔT dans le
référentiel du laboratoire (référentiel impropre pour les évènements [création du muon dans
l’accélérateur de particules ; désintégration du muon dans l’anneau de stockage] est 28,87 fois
plus élevée que la durée de vie des muons ΔT
0
(durée propre mesurée dans le référentiel propre
lié au muon).
Cette durée plus longue leur permet de faire 28,87 fois plus de tours.
28,87×14 = 404 tours
28,87×15 = 433 tours
Ces résultats sont cohérents avec le texte précisant « plus de 400 tours ».
3. Les muons pour la tomographie d’un volcan
3.1. D’après le 2
ème
document, chaque muon perd en moyenne 2 MeV par cm de roche traversé
donc un muon d’énergie moyenne sera totalement absorbé à partir
de :
3
1
4
2 10 cm
2 .
GeV
MeV cm
−
= ×
soit environ 20 m.
Sans faire de mesure précise (rapport d’échelle), le 3
ème
document nous permet de déterminer
que l’épaisseur de roche que les muons doivent traverser en traversant le volcan est bien
supérieure à 500 m (échelle de la carte) donc les muons ordinaires ne peuvent pas être utilisés
pour radiographier la Soufrière (ou tout volcan de diamètre supérieur à 20 m …)
3.2. D’après le 2
ème
document, au niveau du sol, le flux moyen de muons est d’environ 1 muon par
cm
2
et par minute : il faut donc déterminer la surface de la Soufrière.
On ne peut plus échapper à un rapport d’échelle pour déterminer le diamètre moyen du volcan.

2
2
. .
2
D
S R
π π
= =
2
2 2
9 2
9,6 10 10
7,2 10 cm
2
S
π
× ×
= × = ×
(D convertie en cm pour avoir S en cm²)
Il y a donc 7,2×10
9
muons qui arrivent chaque minute sur la Soufrière.
En considérant qu’il s’agit de muons « ordinaires » d’énergie 4 GeV, l’énergie totale est donc :
9 10 10 9 19
7,2 10 4 2,88 10 2,88 10 10 1,60 10
E GeV
−
= × × = × = × × × ×
= 5 J (1 CS en toute rigueur)
Les 7 milliards de muons ont tous ensemble la même énergie que l’énergie cinétique d’une boule
de masse 10 kg allant à 1 m.s
-1
.
2
1
. .
2
C
E mv
=
E
C
=
2
1
10 1
2
× ×
= 5 J.
D 9,2 cm
500 m 4,8 cm
2
9,2 500
9,6 10 m
4,8
D
×
= = ×

3.3. D’après les données, l’énergie d’une particule (relativiste) de masse m en mouvement est
E = γ.m.c
2
, ainsi
2
.
E
mc
γ
=
De plus 1
²
1
²
v
c
=−
γ
2
2
2
1
1
v
c
γ
=−
2
2 2
1
1v
c
γ
− =
2
2 2
1
1
v
c
γ
− =
2
1
1
v
c
γ
= −
2
2
2
2
1 .
1 1
.
v mc
c E
E
mc
= − = −
Pour un muon de masse m
µ
= 105,66 MeV.c
-2
et d’énergie E = 4 GeV = 4×10
3
MeV,
2
3
105,66
1 0,99965 99,965%
4 10
v
c
= − = ≈
×
pour les muons « ordinaires ».
Or les muons utilisés pour la radiographie volcanique sont plus énergétiques donc plus rapides
que les muons « ordinaires » : ils sont donc « ultra-relativistes » car leur vitesse est quasiment
égale à de celle la lumière dans le vide.
Remarque : le même calcul pour un muon d’énergie 1000 GeV donne
9464,32
γ
=
et
0,999999994
v
c
=
.
1
/
4
100%