Temps et relativité restreinte - leprof

Page 1 sur 3
Chap. B4 Temps et relativité restreinte
I. La relativité restreinte
1- Limites de la mécanique classique
En mécanique classique, si deux mobiles A et B se déplacent avec les vitesses
A
v
et
B
v
par rapport à un
référentiel galiléen, pour A, le mobile B se déplace à la vitesse
B
v
-
A
v
.C’est la loi de composition des
vitesses, qui reste vraie pour une onde sonore ou une vague sur la mer.
L'expérience de Michelson et Morley, effectuée en 1887 montre que la vitesse de propagation de la
lumière dans le vide par rapport à la Terre est indépendante de la vitesse de déplacement de la Terre par
rapport au Soleil.
2- Postulats
Albert Einstein publie en 1905, une nouvelle théorie : la relativité restreinte qui s’appuie sur deux
postulats.
- Les lois de la physique s'expriment de la même façon dans tous les référentiels galiléens.
- La vitesse de propagation de la lumière dans le vide est indépendante du mouvement de la source
lumineuse et elle est invariante dans tout changement de référentiel galiléen.
On la note c = 299792458 m.s-1 = 3,00.108 m.s-1
Il existe donc une vitesse limite, égale à la célérité c de la lumière dans le vide, qui ne peut être dépassée
par aucun signal transportant une information, ni aucune particule. Elle ne peut être atteinte que par les
particules de masse nulle comme le photon.
3- Tests expérimentaux
a) Expérience d'Arago
Vers 1810, Arago place un prisme sur le trajet de la lumière émise par différentes étoiles. La déviation
des rayons lui fournit une mesure de la célérité de la lumière incidente, il constate que cette célérité ne
dépend pas du déplacement de l'étoile vis-à-vis de la Terre.
b) Expérience de Michelson et Morley
À la fin du XIXe siècle, Albert Michelson met au point un appareil très sensible qui exploite le
phénomène d'interférence, il veut mettre en évidence les possibles variations de la célérité de la lumière,
selon qu'elle se propage dans la direction du mouvement de la Terre ou dans la direction perpendiculaire.
Aucun effet n'est observé.
c) Expérience de George Joos
En 1930, ce physicien allemand construisit un interféromètre de très grande taille (21 m) tournant
lentement autour d'un axe vertical. Le but était de mesurer la vitesse de la lumière pour différentes
vitesses de la source lumineuse contenue dans l'interféromètre. La même vitesse fut obtenue
indépendamment de la vitesse de l'appareil.
Les dernières expériences en 2009 confirment l’invariance de la célérité de la lumière avec une
incertitude relative de 10-17.

Page 2 sur 3
II. Caractère relatif du temps
Les postulats de la relativité restreinte d'Einstein imposent d'abandonner la conception newtonienne
selon laquelle le temps est une réalité absolue : la mesure du temps dépend du référentiel de mesure.
1- Notion d’évènement.
Un événement est un fait se produisant en un point de l'espace à un instant unique dans le temps.
2- Temps propre.
C’est l’intervalle de temps entre deux événements se produisant en un même lieu, on le note tP
Une durée propre concernant un objet est une durée mesurée par une horloge immobile dans le
référentiel propre de cet objet, on la note tm.
3- Temps mesuré.
Le temps mesuré ou durée mesurée est donné pour un observateur en mouvement par rapport aux
évènements observés
4- Dilatation des durées.
Soit un référentiel propre RP galiléen se déplaçant à la vitesse v par rapport à un autre référentiel galiléen
R.
L’intervalle de temps propre tP entre deux évènements mesuré dans le référentiel RP est toujours plus
court que l’intervalle de temps mesuré tm dans le référentiel R.
tm =  . tP avec
²c²v
1
1
1 coefficient de Lorentz, ou coefficient de dilatation des durées.
tm > tP une horloge qui se déplace par rapport à un observateur bat plus lentement qu’une horloge
immobile par rapport au même observateur
5- Preuves expérimentales
- Dès 1971, on vérifiait que des horloges atomiques embarquées dans des avions se décalaient par
rapport à des horloges restées au sol
- La mesure du temps dans un système de localisation (GPS ou Galileo) est d'une précision telle que la
relativité du temps doit être prise en compte. La bonne marche d'un tel système valide la théorie
d'Einstein.
- Les physiciens des particules étudient le plus souvent des particules dont les vitesses sont proches de c.
La mécanique classique est alors totalement inopérante.
- Des particules instables animées de vitesses proches de c, présentes dans les rayons cosmiques ou les
accélérateurs de particules, peuvent être observées pendant une durée très supérieure à leur durée de vie
propre. C'est une preuve expérimentale de la dilatation des durées. (La création et la désintégration d'une
particule instable constituent deux événements qui ont lieu au même endroit dans le référentiel R où
cette particule est fixe. R est le référentiel propre et l'intervalle de temps mesuré par l'horloge associée à
R est l'intervalle de temps propre.
Mais l'intervalle de temps qui correspond à la durée de vie de cette même particule, mesuré dans le
référentiel terrestre R', est plus grand que l'intervalle de temps propre, du fait de la dilatation des durées.
La courte durée de vie d'un muon (associé à R) produit par collision entre les rayons cosmiques et les
molécules de l'atmosphère ne devrait pas lui permettre d'atteindre le sol. Pourtant, les détecteurs présents

Page 3 sur 3
au sol (associé à R') indiquent la présence de muons, ce qui constitue une preuve de la dilatation des
durées dans le référentiel terrestre)
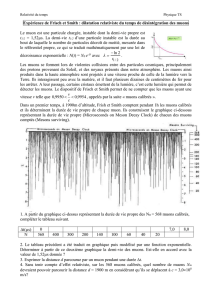
- L'expérience des physiciens Bruno Rossi et David Hall, en, 1941, est la première preuve expérimentale
de la dilatation des durées. Ils ont mesuré le flux des muons au sommet du Mont Washington dans le
New Hampshire aux Etats-Unis, à environ 2000 m d'altitude ainsi qu'à la base de la montagne. En
considérant une demi-vie de 1,56 microsecondes, ils ont observé qu'il y avait 1,4 fois plus de muons au
sommet du Mont Washington que dans la vallée alors que les lois classiques prédisent qu'il devrait y en
avoir 22,3 fois plus en altitude (les muons sont des particules produites dans la haute atmosphère (dues
au bombardement des protons cosmiques) qui se désintègrent spontanément pour donner d'autres
particules.
Dans un référentiel où ils sont au repos, ils se désintègrent de sorte que la moitié des muons a disparu au
bout d'une durée T0 = 1,56 s.
Dans le référentiel terrestre, le trajet des muons entre l'altitude du sommet de la montagne et le niveau de
la mer dure 6,4 s.
Cette durée est supérieure à 4T0 donc, sans considération relativiste, il faudrait s'attendre à ce que la
population de muons soit divisée plus de quatre fois par 2 pendant cette durée.
Or, lorsque 560 muons étaient détectés en altitude, 410 étaient détectés au niveau de la mer.
Sans considération relativiste, il est impossible d'expliquer pourquoi autant de muons atteignent la Terre.
La durée entre les deux événements « Le muon est au sommet de la montagne » et « Le muon atteint le
niveau de la mer » est une durée propre pour le muon, mais une durée impropre pour un observateur
terrestre.
La vitesse de ces particules étant v = 0,995c, le temps nécessaire, dans le référentiel terrestre, pour que la
moitié des muons disparaissent est :
²c²v
1
T
T0
=
²995,01
56,1
=15,6 s
Au bout de 6,4 µs, il est donc normal qu'il en reste plus de la moitié.
6- Contraction des distances
Un raisonnement similaire au temps permet de dire que la longueur propre est supérieure à la longueur
mesurée.
mp  
on appelle  le coefficient de contraction des longueurs tel que  =
1
=
²c²v
1
Et
mp  