Lycée Marcel Rudloff - Académie de Strasbourg

Académie de Strasbourg - GPS "Détecteurs de particules"
Activité : Muons et relativité restreinte – 2013/2014 Page 1
Activité : Muons et relativité restreinte
Le muon dans le modèle standard
Dans le Modèle dit Standard de la Physique des Particules, la matière connue est composée de
quarks et de leptons (12 particules en tout). Ces particules interagissent selon trois types
d’interactions fondamentales dont les médiateurs sont les bosons de jauge. La gravitation, la
quatrième interaction n’est pas intégrée dans le Modèle Standard (Tableau ci-dessous).
Le muon est chargé électriquement (µ+ et µ- particule et antiparticule) donc sensible aux
interactions électromagnétiques. Il est 207 fois plus « lourd » (mμ = 105.66 MeV.c-2 ) que son
cousin l’électron. Une autre différence, le muon « meurt » : sa durée de vie moyenne mesurée dans
son référentiel propre est de τ ≈ 2,197 µs. (une horloge « embarquée » avec le muon indiquerait
2,197 µs).
Et comme indiqué plus haut le muon meurt selon :
Le muon se désintègre en un neutrino muonique et un boson W-. Ce
dernier se désintègre à son tour pour donner un électron et un
neutrino électronique.
1. Quelle est la place du muon dans le modèle standard ?
2. Quelle est l’interaction mise en jeu lors de la désintégration du muon ?
e
e

Académie de Strasbourg - GPS "Détecteurs de particules"
Activité : Muons et relativité restreinte – 2013/2014 Page 2
Détection du muon atmosphérique
A - Le muon est produit par collisions de particules dans les accélérateurs et dans la haute atmosphère par
collisions des particules cosmiques avec les noyaux atomiques composant l'atmosphère.
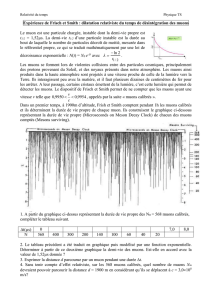
On considère que les muons atmosphériques sont produits à une altitude de 15 km et arrivent à la surface
de la Terre avec une énergie totale moyenne de E = 4,0 GeV après avoir perdu de l'énergie en traversant
l'atmosphère.
1. Calculer classiquement la longueur du parcours d'un muon dans l'atmosphère avant qu'il ne se
désintègre en supposant qu'il se meut à la vitesse de la lumière. Quel est le référentiel considéré ?
2. Déduire que la cinématique classique est insuffisante ?
3. Calculer le facteur de Lorentz
associé au muon sachant que
et E = γ. mμ .c².
4. Calculer la durée de vie moyenne du muon mesurée dans le référentiel terrestre.
5. Répondre à la question 1. dans le cadre de la relativité restreinte. Conclure.
6. Vérifier que l'on a bien .
B - Dans une publication parue en 1963, D.H. Frisch et J.H.
Smith (MIT Massachusetts) exposèrent les résultats d'une
expérience qui confirmait la dilatation des durées annoncée
par Einstein dans le cadre de la théorie de la relativité
restreinte. Ils mesurèrent le nombre N0 de muons détectés par
heure à l'altitude de 1910 m (Mont Washington) et le nombre
N de muons détectés par heure à une altitude de 3.05 m
(Cambridge) en ne sélectionnant que des muons
monocinétiques de vitesse v = 0.9952 c. Ils trouvèrent :
N0 = 563 h-1 ; N = 408 h-1
On montre que, dans le référentiel propre du muon le nombre N0 présents à l’instant t=0 décroit au bout
d’un temps t selon la loi : N=N0 .exp (-t/τ) (1), τ étant la durée de vie moyenne propre du muon.
1. Calculer le nombre de muons par heure N que l'on devrait détecter à Cambridge par des considérations
classiques.
2. Montrer alors que les résultats expérimentaux sont incompatibles avec une application classique de la
formule (1). D’où viendrait l’erreur ?
3. Appliquer (1) dans le cas relativiste pour un observateur terrestre. Conclure.

Académie de Strasbourg - GPS "Détecteurs de particules"
Activité : Muons et relativité restreinte – 2013/2014 Page 3
Mesure de la durée de vie moyenne propre τ du muon
On utilise le détecteur associé au dispositif de la roue cosmique (figure ci-dessous) Certains muons, les
moins énergétiques, peuvent se désintégrer dans le scintillateur donnant lieu à deux signaux successifs -
"start" et "stop" correspondant respectivement à la détection du muon incident et de l'électron produit
selon :
L'électronique permet d'acquérir la durée séparant le "start" et le "stop" c'est à dire la durée de vie d'un
muon qui se désintègre dans le détecteur. Ces derniers ne sont pas les plus nombreux. On obtient une
distribution suffisante de ces durées pour des acquisitions d'une vingtaine d'heures.
On obtient un fichier brut sous le format .txt joint au présent document.
1. Pourquoi faut-il faire des acquisitions sur de longues durées ?
2. Ouvrir le fichier nom.txt à l'aide d'un tableur en décochant toutes les cases à l'exception de tabulation.
3. Créer une colonne t (tableau ci-dessous) regroupant des temps de vie par classes de 500 ns jusqu'à
30000 ns.
4. Créer la colonne N qui donne la fréquence des événements pour chaque classe (taper : fréquence(t;
classes) ctrl & Shift & Entrer.
5. Copier dans le presse papier les colonnes t et N dans Regressi et tracer N= f(t) que l'on modélisera par
N=a+b.exp (-t/τ) .On supprimera la première ligne du tableau (0 ; 0)

Académie de Strasbourg - GPS "Détecteurs de particules"
Activité : Muons et relativité restreinte – 2013/2014 Page 4
6. On montre que la grandeur τ est bien la durée de vie moyenne propre du muon. Conclure.
_______________________________________________________________________________________
Complément :
Le nombre de désintégrations par seconde observées dans une population initiale de N0 muons est donnée par l'activité
, n(t) représente ici le nombre de muons présents à l'instant t. Le nombre de muons se désintégrant dans un
intervalle de temps de largeur Δt (500 ns dans notre cas) correspond au nombre N figurant dans tableau. On montre qu'à partir de
(2) qu'on a bien
K étant une constante.
Le paramètre a intervenant de l'expression de la modélisation correspond au bruit de fond.
Donnée :
c = 3.00 x 108 m.s-1
1
/
4
100%