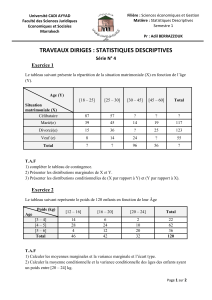
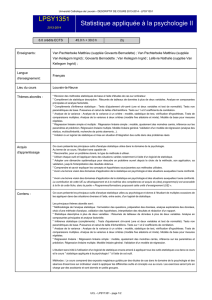
Document

1
Université Abderrahmane MIRA-Bejaia
Faculté des sciences économiques, Commerciales et des Sciences de gestion
Département des sciences de Gestion
Polycopié
Réalisée par: Dr BOUKRIF Nouara
Préparée par Dr BOUKRIF Nouara
Année : 2016
Cours :
Régression Linéaire simple et
multiple

2
Introduction générale du cours Régression linéaire simple et multiple
L’objectif de la régression linéaire simple et multiple est d’apprendre à l’étudiant comment
analyser un phénomène quelconque on utilisant des méthodes statistiques dites économétriques.
En effet, la régression linéaire est une relation stochastique entre une ou plusieurs
variables. Elle est appliquée dans plusieurs domaines, tels que la physique, la biologie, la chimie,
l’économie…etc.
Dans ce cours et dans un premier temps, nous allons introduire la régression linéaire où on
explique une variable endogène par une seule variable exogène. A titre d’exemples, on peut citer :
la relation entre la variable Prix et la variable Demande, la relation entre la variable Revenu et la
variable Consommation, la relation entre la variable Investissement et la variable Croissance
économique. Il s’agit de la régression linéaire régression simple. Dans un deuxième temps, nous
étudierons la régression linéaire multiple qui représente la relation linéaire entre une variable
endogène et plusieurs variables exogènes. Autrement dit, il s’agit de régresser linéairement une
grandeur économique (variable à expliquer) sur plusieurs variables explicatives (variables
exogènes). Par exemple, d’après la théorie économique, la demande d’un produit peut être
expliquée par les grandeurs Prix, Revenu et Publicité.
La régression linéaire simple et multiple est un outil d’analyse qui fait appel à trois
domaines scientifique, à savoir :
 la théorie économique ;
 l’analyse statistique ;
 la modélisation mathématique.
Dans ce polycopié on présentera les différents modèles de régressions linéaires à savoir : le
modèle de régression linéaire simple et multiple.

3
Chapitre : Le modèle de régression linéaire simple
I-1 Définition du modèle de régression linéaire simple
Le modèle de régression linéaire simple est une variable endogène (dépendante) expliquée
par une seule variable exogène (indépendante) mise sous forme mathématique suivante :
ttt XY
 10
,
nt ........1
avec :
t
Y
: la variable endogène (dépendante, à expliquer) à la date t ;
t
X
: la variable exogène (indépendante, explicative) à la date t ;
10 ,
: les paramètres inconnus du modèles ;
t
: l’erreur aléatoire du modèle ;
n: nombre d’observations.
I-2 Hypothèses du modèle
Le modèle repose sur les hypothèses suivantes :
.paramètresaux rapport -par Xen linéaireest modéle le -6
; aléatoire pasest n' exogène variablea5
,0),cov(4
; éesautocorrél passont ne , si ,0cov -3
,)(2
centréeerreur l',0)(1
; exogène variablela avec corrélée pasest n'erreur l'
erreurs les
; ) ticitéhomoscédasd' hypothèse(l' constanteest erreur l' de variancela
,
22
l
xtt
tt
t
t
tt
I-3 Estimation des paramètres par la méthode des Moindres Carrés Ordinaires (MCO)
Soit le modèle suivant :
ttt XY
 10
L’estimation des paramètres
10 ,
est obtenue en minimisant la somme des carrés des erreurs :

4
 n
t
n
ttt
n
ttSMinXYMinMin 1
2
1
2
10
1
2
Pour que cette fonction ait un minimum, il faut que les dérivées par-rapport à
10 et
soient
nuls.
).(
ˆ
ˆ
. et puisque
ˆ
bienou
ˆˆ
:) d (2),et (1) équations des solutions les
ˆ
et
ˆ
notansEn
.....(2)..........0))((20
.....(1)..........0)1(20
11
2
1
11
0
11
0
1
1
1
0
10
1
2
1
1
0
1
10
1
1
1
10
11 10
0
:obtienton , (2)équation l' dans de valeur la remlaçant En
(1 après'obtient on
n
tt
n
tt
n
ttt
n
tt
n
tt
n
tt
n
tt
n
tt
n
tt
n
ttt
n
tttt
n
tt
n
tt
n
tt
n
ttt
XXXXYXY
X
n
X
Y
n
Y
XnY
n
X
n
Y
XXXYXXY
S
XnYXY
S
D’où
2
2
1
1
1
22
1
1 1
2
1 1
1
ˆ
tt
t
n
tt
n
tt
n
ttt
n
t
n
ttt
n
t
n
tttt
XX
XXYY
XnX
XYnYX
XXX
XYYX

5
Conclusion : les estimateurs des MCO du modèle de régression linéaire simple
ttt XY
 10
Sont :
ˆ0XnY 
Et
2
2
1
1
1
22
1
1
ˆ
tt
t
n
tt
n
tt
n
ttt
XX
XXYY
XnX
XYnYX
Différentes écritures du modèle de régression linéaire simple :
Le modèle théorique ( modèle non ajusté) :
ttt XY
 10
Le modèle estimé ( modèle ajusté) :
ttt eXY  10 ˆˆ
Avec :
t
Y
ˆ
=
t
X
10 ˆˆ
Et
ttttt XYYYe 10 ˆˆ
ˆ
t
e
: est le résidu du modèle.
Exemple : nous disposons des données qui sont représentés dans le tableau suivant :
t
X
100
200
300
400
500
600
700
t
Y
40
50
50
70
65
65
80
Où
t
Y
désigne les quantités consommées et
t
X
désigne le prix des quantités consommées.
On trace un graphique des couples de données liant le prix et les quantités Consommées. Nous