1 Introduction. 2 Description du convertisseur.

rencontre du non-lin´ eaire 2005 1
Mod´elisation en temps discret d’un convertisseur d’´energie ´electrique.
Bruno Robert,AbdelaliElAroudi,MauriceFadel
Universit´e de Reims Champagne-Ardenne
CReSTIC-DeCom, Moulin de la Housse, BP 1039, Reims Cedex 2, France
[email protected]
R´esum´e
Cet article montre comment pr´edire les bifurcations dans le fonctionnement d’un
hacheur abaisseur `a deux cellules et comment analyser la route suivie vers le chaos
en utilisant un mod`ele non lin´eaire en temps discret. Le comportement global est
´etudi´e au moyen de diagrammes de bifurcation montrant les points fixes stables et
des fronti`eres dans l’espace. Les points d’´equilibre et leur stabilit´e sont examin´es de
mani`ere analytique. Les bifurcations par collision de fronti`eres ont leur origine dans
les saturations du modulateur MLI.
Abstract
By using a non linear discrete time model, this paper shows how to predict bifurcations in a 2 cells
chopper and analyses the road to chaos. Equilibrium points and their stability are investigated in an
analogical way to determine the nature of the bifurcations. The global behaviour is studied by using
bifurcation diagrams showing collisions between fixed points and border lines. The border collision
bifurcations have their origin in the saturations of the PWM modulator.
1 Introduction.
Dans tous les domaines industriels, les convertisseurs statiques jouent un rˆole essentiel
dans la conversion d’´energie. Une activit´e de recherche croissante concerne actuellement les
convertisseurs multicellulaires car, pourvus d’un contrˆole appropri´e, ils sont bien adapt´es
au conditionnement des sources d’´energies renouvelables. De plus, en raison de leur struc-
ture modulaire, ils peuvent ˆetre associ´es tr`es facilement [1].
Au cours des derni`eres ann´ees, on a d´ecouvert que la plupart des convertisseurs sta-
tiques ´etaient le si`ege de ph´enom`enes non lin´eaires m´econnus en ´electronique de puissance.
En dehors de leurs r´egimes de fonctionnement normaux, au sens de l’ing´enierie, les conver-
tisseurs multicellulaires peuvent eux aussi exhiber des comportements insolites parfois
chaotiques. Or les mod`eles moyens habituels ne permettent pas de pr´edire les ph´enom`enes
non lin´eaires rencontr´es. Par nature, ces mod`eles masquent les non lin´earit´es essentielles
[2]. Pour analyser, pr´edire et contrˆoler ces comportements ´etranges, il est n´ecessaire de
disposer de mod`eles non lin´eaires en temps discret [3, 4].
2 Description du convertisseur.
Le convertisseur ´etudi´e est repr´esent´e sur la figure 1. Il est con¸cu `a partir d’un hacheur
s´erie modifi´e pour supporter une tension d’entr´ee plus ´elev´ee. Deux commutateurs sont
associ´es en s´erie et un condensateur ´equilibre la r´epartition de la tension entre eux. Une
commande appropri´ee en Modulation de Largeur d’Impulsion (MLI) permet `alafoisde
maintenir la charge du condensateur `a une valeur proche de la demi-tension d’entr´ee
c
Non Lin´eaire Publications,Bˆat.510, Universit´e de Paris-sud, 91405 Orsay

2B.Robert, A.El Aroudi, M.Fadel
et de contrˆoler le courant dans la charge. La figure 1 montre aussi l’organisation de la
commande et les signaux de contrˆole des transistors d´elivr´es par le modulateur MLI. Le
cycle de fonctionnement s’´etablit sur 4 intervalles de temps comme le montre la figure 2.
Intervalle 1 : u1=0,u
2=1.D´echarge du condensateur dans le r´ecepteur inductif.
Intervalle 2 : u1=1,u
2= 1. Charge de l’inductance et maintien de la tension.
Intervalle 3 : u1=1,u
2= 0. Charge du condensateur `a travers le r´ecepteur inductif.
Intervalle 4 : Idem intervalle 2 mais la dur´ee peut ˆetre diff´erente.
3Mod´elisation.
Le mod`ele est ´elabor´e dans un espace d’´etat sans dimension. Le vecteur d’´etat est
not´eX=iv
tdans lequel vest la tension sur le condensateur r´eduite par rapport `a
la tension d’alimentation Eet iest l’intensit´educourantr´eduite par rapport au courant
maximal E/
R.L’´evolution est d´ecrite sur chaque intervalle par un syst`eme diff´erentiel
lin´eaire `a coefficients constants : ˙ X=AkX+Bk,k∈{1,2,3,4}. Le temps, sans dimension,
est r´eduit par rapport `alap´eriode fondamentale T.Lemod`ele en boucle ouverte est obtenu
en int´egrant sur chaque intervalle de temps et en raccordant les solutions aux instants de
commutation pour obtenir une r´ecurrence de la forme : xn+1 =ϕ(d1,d2)·xn+ψ(d1,d2).
Les commutateurs sont command´es par un modulateur MLI num´erique. Le courant
et la tension sont ´echantillonn´es en d´ebut de p´eriode pour ´evaluer l’erreur de courant
εi=in−Iret l’erreur de tension εv=vn−1
2dans lesquels Iret 0.5 sont les consignes. Le
contrˆoleur calcule la loi de commande d´eduite de [5] pour d´eterminer les rapports cycliques
(a)
Fig. 1–(a) Hacheur abaisseur `a 2 cellules. (b) Contrˆoleur de tension et de courant.
Fig. 2–Cycle de fonctionnement en r´egime permanent.

Mod´elisation non lin´eaire d’un convertisseur multicellulaire. 3
d1et d2:d1,2(Xn)=kiεin ±kvεvn dans laquelle ki>0etkv>0 sont les gains en courant
et en tension. En posant δL=RT
L1etδC=T RC 1defa¸con `ar´eduire l’ondulation
ducourantetdelatension,onpeutlin´eariser les exponentielles de matrice et obtenir le
mod`ele en boucle ferm´ee sous la forme d’une r´ecurrence non lin´eaire bidimensionnelle :
Xn+1 =1−δL(1 + ki)2δLkv(vn−1)
−2δCkv(vn−0.5) 1 Xn+δL1+kiIr+kv
2
0
Le r´egime de fonctionnement normal correspond au point fixe, not´e X∗
1:X∗ 1=
[i∗
1,v∗ 1]t=1+kiIr
1+ki,1 2t.Ilestind´ependant de L. La matrice jacobienne est :
J(X)=1−δL(1 + ki)2δLkv(2vn−1)
−2δCkv(vn−0.5) −2δCkvin+1 .
Evalu´ee au point d’´equilibre X∗
1,Jest diagonale. En supposant que kv<1
δC,alors
|−2δCkvi∗
1+1|<1 quel que soit i∗ 1.Onend´eduit la condition de stabilit´edupoint
fixe : 0 <k
i<2
δL−1 et on note ki1la limite de stabilit´edeX∗
1:ki1=2L−1.
4 Comportement global.
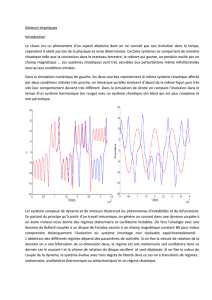
Les diagrammes de bifurcation de la figure 3 rendent compte du comportement global
du convertisseur lorsque l’inductance ou le gain en courant varient. Les param`etres sont :
IR=0.6, kv= 1, E=1, R=1, L=10, C=40, F=1 donc δL=0.1, δC=0.1.
Le premier diagramme est obtenu avec un gain en courant constant ki=15etlepa-
ram`etre de bifurcation est l’inductance L. Sur sa droite, le convertisseur pr´esente un r´egime
p´eriodique fondamental (T= 1) qui est le plus important du point de vue de l’ing´enierie.
Le point fixe est effectivement ind´ependant de L. Cependant, en de¸c`adelalimitedesta-
bilit´eL=8,unr´egime de p´eriode 2 stable apparaˆıt. En r´eduisant encore l’inductance, un
nouveau mode de fonctionnement apparaˆıt, le courant alternant `a l’int´erieur de 4 bandes
chaotiques.
Le second diagramme est calcul´e avec une inductance constante L=10etlepa-
ram`etre de bifurcation est le gain en courant ki. Sur sa gauche, le convertisseur pr´esente
son r´egime de fonctionnement normal avec un point de fonctionnement stable se rappro-
chant de la r´ef´erence lorsque le gain augmente. Au-del`a de la limite de stabilit´eki= 19,
un doublement de p´eriode se manifeste puis un r´egime de fonctionnement chaotique.
(a) 6 6.5 7 7.5 8 8.5 9 9.5 1
0
0.54
0.56
0.58
0.6
0.62
0.64
0.66
0.68
L
in
Transitoire : 1000 Affichage : 300 I
r=0.6, ki=15, C=10, kv=1
Frontière supérieure
Frontière inférieure
(b) 15 20 25 3
0
0.57
0.58
0.59
0.6
0.61
0.62
0.63
0.64
0.65
0.66
0.67
ki
in
Transitoire : 1000 Affichage : 300 I
r=0.6, L=10, C=10, kv=1
Frontière supérieure
Frontière inférieure
Fig. 3–Diagrammes de bifurcation du courant (a) Variation de L (b) Variation de ki.

4B.Robert, A.El Aroudi, M.Fadel
Il est important de noter que nous avons ici affaire `a des bifurcations non standard.
On n’observe pas de cascade de doublements de p´eriode avec un point d’accumulation
conduisant au chaos mais seulement un doublement de p´eriode pr´esentant une discontinuit´e
imm´ediatement suivi d’une bifurcation directe vers le chaos. La section suivante s’attache
`a montrer que l’une comme l’autre sont des bifurcations par collisions de fronti`eres.
5Mod`ele avec saturations.
Dans cette section nous proposons un mod`ele am´elior´e du modulateur MLI prenant
en compte la saturation naturelle des rapports cycliques : d1,2∈[0,1]. Cette approche est
essentielle pour expliquer la route inhabituelle vers le chaos observ´ee sur les diagrammes
de bifurcation.
Les saturations du modulateur font apparaˆıtre deux lignes fronti`eres qui divisent
l’espace d’´etat en trois r´egions. Dans chaque r´egion, le convertisseur est mod´elis´e par une
r´ecurrence sp´ecifique.
En premier lieu, on consid`ere la saturation basse. Dans ce cas, le courant ´echantillonn´e
est suffisamment petit pour que les deux transistors restent passants durant toute la
p´eriode : d1=d2=0.D’o`ulafronti`ere basse : εi=0⇒in=Ir. Le deuxi`eme cas se
pr´esente quand le courant est assez grand pour que les deux transistors soient bloqu´es sur
toute la p´eriode : d1=d2=1.D’o`ulafronti`ere sup´erieure : εi=1
ki⇒in=Ir+1 ki.Par
cons´equent, le mod`ele par morceaux est le suivant :
Xn+1 =F(Xn)=⎧
⎨
⎩
F1(Xn)=A01Xn+B0si in≤Ir
F2(Xn)=AXn+Bsi Ir≤in≤Ir+1
ki
F3(Xn)=A01Xnsinon
o`u: A01 =1−δL0
01
,B0=δL
0,A=1−δL(1 + ki)2δLkv(vn−1)
−2δCkv(vn−0.5) 1 et
B=δL1+kiIr+kv
2
0.
En utilisant ce nouveau mod`ele, il est possible d’´etudier les conditions d’existence du
point fixe X∗
1. Nous avons vu dans la section 3 que ∀ki>0,i
∗
1(ki)>I
r.Deplus,ilest
facile de v´erifier que ∀ki>0,i
∗
1(ki)<I
r+1
ki. On en conclut donc que le point fixe X∗
1
est situ´e entre les deux fronti`eres, qu’il existe sur l’intervalle 0∞et qu’il est stable
sur l’intervalle 0ki1.
6 Doublement de p´eriode.
Un mode de fonctionnement avec une p´eriode double s’´etablit apr`es la d´estabilisation
de X∗
1. Il est caract´eris´e par les deux points fixes de la r´ecurrence Xn+2 =F2◦F1(Xn).
Le premier point d’´equilibre, not´eX∗
2,est:X∗ 2=[i∗ 2,v∗ 2]t=ki(Ir−δL)+2−δL
ki(1−δL)+2−δL,1
2t
.
Le second point fixe est : F1(X∗
2)=kiIr(1−δL)+2−δL
ki(1−δL)+2−δL,1
2t
.
Au point de bifurcation : ⎧
⎨
⎩
X∗
2=Ir,1
2t
F1(X∗
2)=Ir(2−3δL+δ2
L)+2δL−δ2 L
2−δL,1 2t.
Puisque Ir<1alorsi∗
2<F
1(i∗
2). Cette bifurcation est donc toujours discontinue.
Elle peut ˆetre interpr´et´ee de la mani`ere suivante. Au point de bifurcation ki1, le point fixe

Mod´elisation non lin´eaire d’un convertisseur multicellulaire. 5
X∗
1perd sa stabilit´e, le multiplieur caract´eristique passant par la valeur -1. Le courant
´echantillonn´e alterne alors entre deux valeurs qui divergent jusqu’au moment o`u l’une
d’entre elles entre en collision avec l’une des deux fronti`eres. A ce moment, la r´ecurrence
de second ordre devient valide.
La matrice jacobienne est la suivante :
J(X)=1−δL(1 + ki)2δLkv(2vn−1)
−2δCkv(vn−0.5) (1 −δL)2δLδCkv(in−1) + 1 −2δCkv.
Evalu´ee au point d’´equilibre X∗
2,Jest diagonale. En supposant que kv<1
δC(1+δL),alors
|2δLδCkv(i∗
2−1) + 1 −2δCkv|<1 quel que soit i∗ 2. Cela conduit `a la condition de stabilit´e:
ki1<k
i<1+(1−δL)2
δL(1−δL)et on note ki2la limite de stabilit´edeX∗
2:ki2=L2+(L−1)2
L−1.
On en conclut que le point fixe X∗
2entre en collision avec la fronti`ere exactement
lorsque le point fixe X∗
1perd sa stabilit´e. X∗ 2existe dans l’intervalle ki1∞et il est
stable sur l’intervalle ki1ki2.
7 Quatre intervalles chaotiques.
Des points fixes de p´eriode 4T apparaissent apr`es la d´estabilisation de X∗
2et sont
instables sur tout leur domaine d’existence. Le diagramme de bifurcation de la figure 3b
illustre le ph´enom`ene. Au-del`adeki2,l’´emergence de ces nouveaux points fixes instables
g´en`ere un comportement chaotique. Les it´er´es se r´epartissent sur quatre intervalles denses
not´es 1, 2, 3 et 4, dans l’ordre croissant des valeurs des it´er´es le long de ces intervalles. Les
quatre intervalles sont visit´es alternativement dans l’ordre suivant : 1-3-2-4. On remarque
que la fronti`ere basse divise l’intervalle 2 en deux sous-intervalles. Selon la position de
l’it´er´e dans cet intervalle, en-dessous ou au-dessus de Ir,deuxformesdelar´ecurrence de
quatri`eme ordre s’appliquent :
Xn+4 =F2121 =F2◦F1◦F2◦F1(Xn)siin+2 <I
r
F2221 =F2◦F2◦F2◦F1(Xn)siin+2 >I
r
En ce qui concerne le point fixe de F2121 et sa stabilit´e, les r´esultats sont identiques
`a ceux de F21. Il est donc instable pour tout ki>k
i2.
Au point de bifurcation ki=ki2, le nouveau point fixe X∗
4de F2221 apparaˆıt.Ilest
toujours instable. Nous sommes en pr´esence d’une bifurcation entre une solution p´eriodique
2T et une solution chaotique sur quatre intervalles et cette bifurcation est discontinue.
8 Simulations
Avec les mˆemes valeurs num´eriques que pr´ec´edemment, on d´etermine les conditions
de validit´edel’´etude : Ir>0.474 et kv<9.09. Les points de bifurcation sont : ki1=19et
ki2=20,11.
La figure 4 pr´esente une simulation r´ealis´ee avec PSIM. Les param`etres de contrˆole
sont Ir=0.6, kv=1etkibalaye lentement l’intervalle [15,30]. Ce diagramme suit le dia-
gramme th´eorique de la figure 3 calcul´e`a l’aide de Matlab. Les points de bifurcations sont
`apr´esent pr´edits en ki1=20.1etki2=21.5. En raison de la lin´earisation des exponen-
tielles de matrices au cours de la mod´elisation, les r´esultats simul´es diff`erent l´eg`erement
des r´esultats th´eoriques mais en demeurent n´eanmoins tr`es proches.